Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Algebraic Thinking Homework
Session 1, Homework
Problem H1
Many people wonder whether students need to know algebra in order to be successful in today’s world. What do you think? Look at the suggested readings and research some of the arguments on both sides of the issue. Is “Algebra for Everyone” a worthwhile goal?
Problem H2
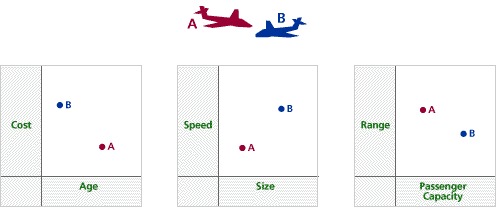
The following quick sketch graphs describe two light aircraft, A and B (note: the graphs have not been drawn accurately):
- The first graph shows that aircraft B is more expensive than aircraft A. What else does it say?
- Are the following statements true or false?
1. The older aircraft is cheaper.
2. The faster aircraft is smaller.
3. The larger aircraft is older.
4. The cheaper aircraft carries fewer passengers. - Copy the graphs below. On each graph, mark and label two points to represent A and B.
Take It Further
Problem H3
Draw sketch graphs for the following sequence of bottles.
Using your sketches, explain why a bottle with straight sloping sides does not give a straight line graph (that is., explain why the ink bottle does not correspond to graph G in Problem C9).
Is it possible to draw two different bottles that give the same height-volume graph? Try to draw some examples.
Tip: For the first problem, think about the overall graph, not just what each piece will look like. What would the graph look like if there were 100 different segments to the bottle? To answer “yes” to the second question requires only one example, so try as many different possibilities as you can before giving up. Consider looking up Cavalieri’s Principle in a geometry textbook.
Problems H2 and H3 taken from The Language of Functions and Graphs, by Malcolm Swan and the Shell Centre Team (Nottingham, U.K.: Shell Centre Publications, 1999), p. 986.
Suggested Reading
Edwards, Edgar L., Jr., ed. Algebra for Everyone
Reproduced with permission from Algebra for Everyone, © 1990 by the National Council of Teachers of Mathematics. All rights reserved.
Download PDF File:
Chapter 2, part 1
Chapter 2, part 2
Chapter 2, part 3
Chapter 3, part 1
Chapter 3, part 2
Chapter 4, part 1
Chapter 4, part 2
Chapter 5, part 1
Chapter 5, part 2
Chapter 6, part 1
Chapter 6, part 2
Chapter 7, part 1
Chapter 7, part 2
Dudley, Underwood. “Is Mathematics Necessary?”
Reproduced with permission from The College Mathematics Journal, © 1997 by the Mathematical Association of America. All rights reserved.
Download PDF File:
Riley, Richard W. “Mathematics Equals Opportunity.”
Reproduced with permission from Mathematics Equals Opportunity, © 1998 by the National Council of Teachers of Mathematics. All rights reserved.
Solutions
Problem H2
- It also says aircraft B is newer than aircraft A.
- Are the following statements true or false? 1. 1. True. The older aircraft (A) is cheaper 2.
2. False. The faster aircraft (B) is not smaller.
3.False. The larger aircraft (B) is not older.
4. True. The cheaper aircraft (A) carries fewer passengers. - Copy the graphs below. On each graph, mark and label two points to represent A and B.
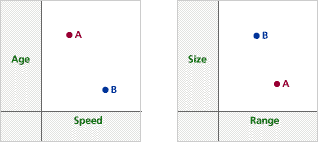
In the first graph, A is in the upper left (high age, low cruising speed), and B is in the lower right (low age, high cruising speed).
In the second graph, A is in the lower right (small size, higher range), and B is in the upper left (big size, slightly smaller range).
Problem H3
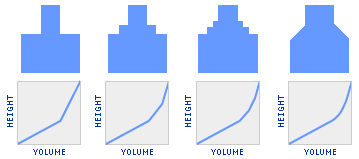
It is possible to draw two different bottles that have the same height-volume graph. A hint: Think about the shapes of bottles you might find in a glass-blowing store, and how you might hold the same amount of liquid in a differently-shaped bottle. Or look up Cavalieri’s Principle online!
A discussion of why a bottle with straight sloping sides does not give a straight line graph is presented in the Homework Review in Session 2. See Note 1.
