Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
More Nonlinear Functions Part A: Cyclic Functions (50 minutes)
Session 8, Part A
In This Part
- Tides
- Heartbeats
Tides
The following situation describes a new kind of function:
Note 2
The ocean has high tides and low tides. The tide comes in for six hours (ending at “high tide”) and then goes out for six hours (ending at “low tide”). This is repeated twice in a day. An approximate rule to describe the motion of the tide is this:
From low to high tide:
In the first hour, 1/12 of the tide comes in.
In the second hour, 2/12 of the tide comes in.
In the third hour, 3/12 of the tide comes in.
In the fourth hour, 3/12 of the tide comes in.
In the fifth hour, 2/12 of the tide comes in.
In the sixth hour, 1/12 of the tide comes in.From high to low tide:
In the first hour, 1/12 of the tide goes out.
In the second hour, 2/12 of the tide goes out.
In the third hour, 3/12 of the tide goes out.
In the fourth hour, 3/12 of the tide goes out.
In the fifth hour, 2/12 of the tide goes out.
In the sixth hour, 1/12 of the tide goes out.
Let’s say the height at low tide is zero and at high tide is 24 feet.
Problem A1
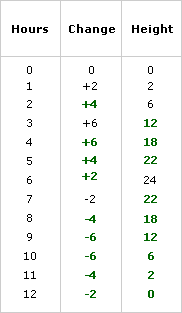
Fill out this table, showing the height of the tide as it comes in and rolls out.
|
|
Tip: Remember that full tide is 24 feet while calculating the tide for each hour.
Problem A2
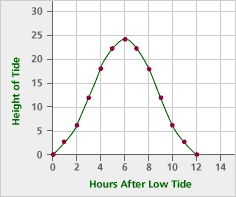
Make a graph of the hours after low tide vs. the height of the tide. Connect the points with a smooth curve.
Problem A3
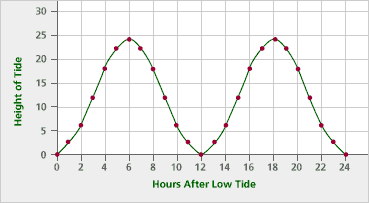
Extend your graph to show a full day (24 hours) of tides.
Tip: Think carefully about what would happen during the second 12 hours.
Problem A4
Describe how this graph is different from graphs of linear, exponential, and quadratic functions you’ve seen.
Functions like the one you just graphed here are called cyclic functions, also known as repeating or periodic functions. These functions are characterized by outputs that repeat in a cycle. Cyclic functions are important in astronomy (they’re used to describe the motion of the planets), engineering, and many other fields.
Two important characteristics of cyclic functions are amplitude and period. The amplitude measures the height of the graph. It’s defined this way:
amplitude = (highest point – lowest point) / 2
The period of a cyclic function is how long it takes to complete a cycle.
Problem A5
What is the period of the graph in Problem A3?
|
Video Segment In this video segment, the cyclic function presented in Part A is graphed. The class then discusses the definitions of amplitude and period. Watch this segment after you’ve worked on Problems A1-A5. If you get stuck on the problems, you can watch the video segment to help you. Think of some other cyclic functions you might encounter in everyday life. What are their periods? You can find this segment on the session video, approximately 4 minutes and 3 seconds after the Annenberg Media logo. |
|
Video Segment In this video segment, taken from the “real world” example at the end of the Session 8 video, Rick Garnen of the Massachusetts Maritime Academy talks about the causes and effects of tides on currents in Cape Cod Bay and how this relates to the mathematics of cyclic functions. You can find this segment on the session video, approximately 23 minutes and 8 seconds after the Annenberg Media logo. |
Tide problem adapted from Trigonometry, by I. M. Gelfand and Mark Saul (Boston: Birkhauser Publishing Ltd., 2001). ISBN:0-8176-3914-4.M
Heartbeats
When your heart beats, it pumps blood throughout your system of arteries. When doctors measure blood pressure, they usually measure the pressure of the blood in the artery of the upper arm.
But your blood pressure isn’t constant. The graph below shows how blood pressure changes over time.
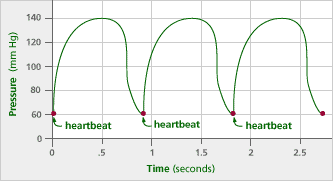
Problem A6
What can you tell about blood pressure just before a heartbeat? Note 3
Problem A7
What happens to blood pressure after a heartbeat?
Problem A8
Is this the graph of a cyclic function?
Problem A9
What are the period and amplitude for this graph?
Heartbeat problem taken from Ups and Downs. Mathematics in Context (Chicago: Encyclopedia Britannica, Inc., 1998), p. 26.
Notes
Note 2
Have graph paper readily available. Before starting work on Problems A1-A5, keep in mind that the graph will have the height of the tide on the y-axis. The “change in tide” column in the table is just to help you create the third column. The computations, though they deal with fractions (multiples of 1/12), should not be difficult, because the height of the tide is a multiple of 12.
Groups: Share graphs by tracing them on overheads. Discuss how this problem is an example of a cyclic function. Think of other examples of things that go in cycles. Examples include the motion of the planets and radio waves.
Think about the concepts of amplitude and period, two ideas that are an important part of the study of cyclic functions. Depending on where you are, the amplitude of tides can vary greatly, although the period is always the same.
Groups: If time allows, sketch graphs for tides in different places around the world. Discuss what would vary and what wouldn’t.
Note 3
Move on to Problems A6-A8. Spend just a few minutes working on these. Take your pulse, and then mark numbers on the time axis as if it were your own heartbeat. Find the period of your own heartbeat function.
Groups: After working on the heartbeat problems, discuss the idea of period again. Finally, add cyclic functions to the list of nonlinear functions you started in the previous session.
Solutions
Problem A1
Problem A2
Problem A3
Problem A4
The graph is not linear, because it’s not a straight line, and the difference between consecutive outputs is not constant. The graph is also not exponential, because it does not increase or decrease indefinitely, and the ratio between consecutive outputs is not constant. Neither is the graph quadratic, because the difference between consecutive outputs is not linear, nor are the second differences constant.
Problem A5
The period is 12 hours.
Problem A6
Blood pressure drops quickly, and appears to be lowest just before a heartbeat.
Problem A7
After a heartbeat, blood pressure increases drastically and peaks quickly.
Problem A8
Yes, this is a cyclic function, because its outputs are repeated consistently over time. The period is one heartbeat.
Problem A9
The period is the length of one hearbeat, which can be measured in seconds or fractions of a minute. In this graph, the period is about 0.9 seconds. The amplitude is half the difference in pressure from the lowest point to the highest point, usually measured in mm Hg (millimeters of mercury), and in this graph is (140 – 60)/2, or 40 mm Hg.
