Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Slope is an important concept in mathematics, and in Part B we’ll explore how it is used to solve problems. Note 5
Take a minute to think about what you already know about slope. What does it mean? Where is it used?
You may be familiar with the idea of slope as a measure of steepness. The formula for slope is usually described as:
slope = (change in y) / (change in x)
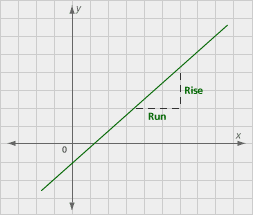
The slope of a line is often described as a ratio of rise/run. Another way to think of slope is as the amount that the dependent variable changes for each increase by 1 in the independent variable. In other words, as x changes by 1, what happens to y?
Look at these four graphs. For each graph, select four pairs of points, and calculate the slope of the line between each pair of points. Remember that slope = (change in y) / (change in x). As you calculate the slopes for each of the graphs, ask yourself why the slope between pairs of points would change or why it would stay the same. Note 6
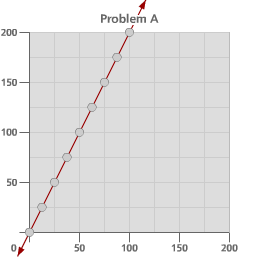
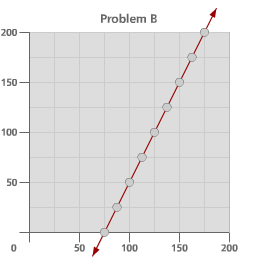
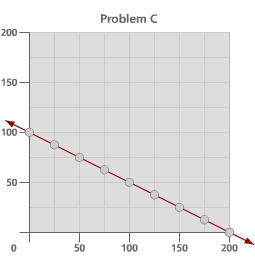
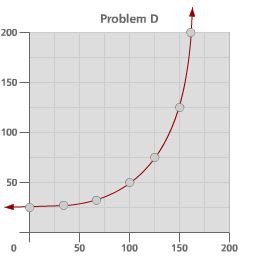
What happened when you tried to find the ratio of rise/run for the fourth example, a curved object?
The drawing below shows a cable attached to a wall.
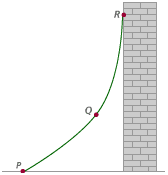
Calculate the ratio rise/run for each pair of points:
Note 7
Describe the difference between the rise/run ratios for the graph in Problem B3 and the ratios for the graph of a line.
Note 8
Here are graphs of nine different lines. Look at the equation and the slope of each line. What changes when the slope becomes positive or negative, and when slope is larger or smaller than 1?
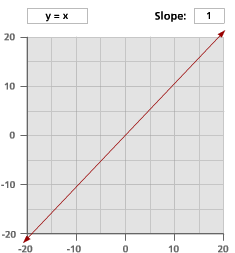
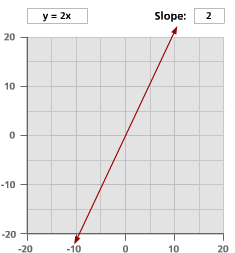
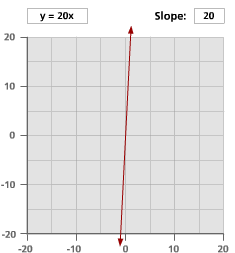
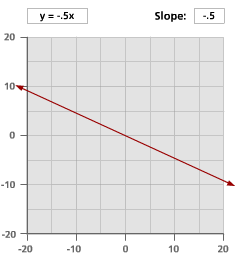
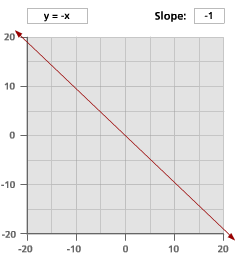
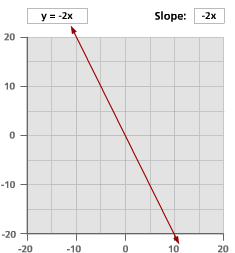
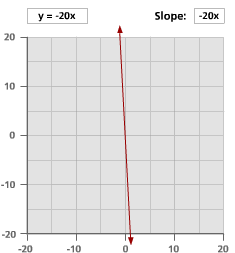
Problem B5
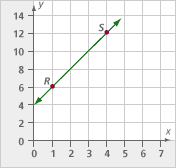
Consider this line. What are the coordinates of the points R and S?
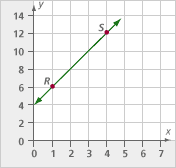
Problem B6
Find the slope of the line through points R and S.
Problem B7
Many people describe “slope” as a measure of the “steepness” of a line. Look at the two graphs below. Which line has larger slope? Which line appears to be steeper? Explain what is happening. Note 9
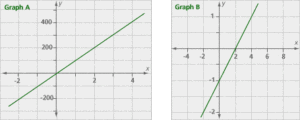
Tip: Is there anything about the graphs that makes comparison more difficult?
|
Video Segment In this video segment, the onscreen participants discuss methods of comparing the slope of two lines. Watch this segment after you have completed Problem B7 and compare your methods of comparison with those of the onscreen participants. If two graphs are drawn with the same scale, is it true that the graph that appears steeper has the larger slope? You can find this segment on the session video, approximately 11 minutes and 32 seconds after the Annenberg Media logo. |
Do the following problems on graph paper:
Problem B8
On one graph, create three different lines with slope 2. Describe what is the same and what is different about these graphs. Note 10
Problem B9
On one graph, create three different lines with negative slope. Describe what is the same and what is different about these graphs.
Problems B5 and B6 taken from IMPACT Mathematics Course 3, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p. 27.
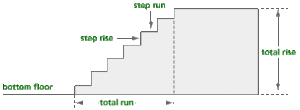
Architects and carpenters use rise and run to describe and build staircases. The picture below shows the rise and run for each step and the total rise and run for the staircase.
Problem B10
An architect is designing a staircase for a house with a difference of 10 feet between floors. The staircase has 18 steps and a total run of 14 feet. What is the ratio (total rise/total run) of the staircase?
Problem B11
Find the rise and run for each step (what we’ll call the step rise and run) in inches. What is the ratio (step rise/step run)? Explain your answer.
Problem B12
Find a nearby staircase and measure the rise and run of one step. How could you use this to estimate the total rise and run of the staircase?
Problem B13
Design a staircase with a total rise of 14 feet, a step rise between 6 and 8 inches, and a sum of step rise and step run between 17 and 18 inches. All steps should have the same rise and the same run. Your answer should include
Tip: There are many different solutions to this problem. Remember that the total of the step rise and the step run must be between 17 and 18 inches.
|
Video Segment In this video segment, taken from the “real world” example at the end of the Session 5 video, master carpenter Norm Abram describes the importance of slope in construction. Watch this segment after completing Part B. In what other professions is slope used on a regular basis? You can find this segment on the session video, approximately 21 minutes and 8 seconds after the Annenberg Media logo. |
Problems B10-B13 taken from IMPACT Mathematics Course 3, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p. 41. www.glencoe.com/sec/math
Note 5
Groups: Discuss what everyone already knows about slope. Go over the definition of slope in the course materials, and then work on Problems B1-B4. Graph paper is needed for this exercise.
Note 6
While working with the first Interactive Activity, choose different pairs of points. For each pair, it’s important that the difference between the y coordinates and the difference between the x coordinates are computed by considering the pairs in the same order. That is, for points (x1, y1) and (x2, y2), the slope can be computed as either
(y1 – y2) / (x1 – x2) or (y2 – y1) / (x2 – x1).
Note that students sometimes confuse this by computing (y2 – y1) / (x1 – x2).
Note 7
For Problem B3, consider measuring directly on the picture or tracing the picture onto graph paper to compute the ratios.
Note 8
Think about the main points for this part of the session: The rise/run for a line is the same between any pair of points on the line; lines are the only kind of graph for which this is true.
Note 9
Problem B7 focuses on the relationships between slope, scale, and the appearance of a line’s graph. It’s an important idea that slope only relates to “steepness” if you are comparing two lines with the same scale.
Note 10
In Problem B8, participants should notice that the lines are all parallel and therefore do not intersect. You may want to talk briefly about what they know about parallel lines, as we will return to this idea in future sessions.
Problem B1
On a basic level, slope measures vertical change over some horizontal distance — a road can “slope up” or “slope down.” The slope of a line describes how much vertical change (change in y) there is per horizontal change (change in x).
Problem B2
On a line, the ratio of rise to run is always constant; on a curved object, this value is constantly changing. So, the slope of a curved object changes depending on the points selected, while the slope of a line is always constant.
Problem B3
From P to Q, the ratio is roughly 0.6.
From P to R, the ratio is roughly 1.3.
From Q to R, the ratio is roughly 4.
Problem B4
The ratios for the graph of a line would be constant throughout. For example, a line connecting P to R would have a rise/run ratio of 1.3, regardless of where a new point was located on it. This is different from the graph used in Problem B3, which has a slope that varies depending on which two points are used.
Problem B5
The coordinates are R(1, 6) and S(4, 12).
Problem B6
The slope is (change in y) / (change in x). The change in y is 12 – 6 = 6, and the change in x is 4 – 1 = 3. Therefore, the slope is 6/3 = 2. Note that the line may not appear to have slope 2, since the vertical axis is labeled by twos, while the horizontal axis is labeled by ones.
Problem B7
Graph A has a larger slope, even though graph B appears steeper. This appearance is caused by the different scale used in the two graphs. If it were placed on the other scale, the line in graph B would appear nearly flat!
Problem B8
All the lines have the same slope at all points. None of the lines intersect, and they are always the same distance from each other — they are all parallel lines.
Problem B9
A line with negative slope travels down and to the right (“decreasing”). Lines with negative slope may still intersect one another. Any line with negative slope will travel through the top left and bottom right quadrants of the graph paper.
Problem B10
The total rise / total run is 10/14, which is roughly 0.71.
Problem B11
To calculate step rise and run, divide both rise and run by 18. The step rise is 10/18 feet (6 2/3 inches) and the step run is 14/18 feet (9 1/3 inches). The ratio of step rise / step run is (10/18) / (14/18), which again equals 5/7 or 0.71 — the step rise and step run are in proportion to the total rise and total run.
Problem B12
The total rise and run can be estimated accurately by multiplying the rise and run of a single step by the total number of stairs, because each stair has roughly the same rise and run.
Problem B13
There are a lot of answers here!
Number of steps: between 21 and 28
Height of each step: between 6 and 8 inches
Run of each step: between 9 and 12 inches
Total run: between 189 and 336 inches
Ratio of step rise to step run: between 6/12 and 8/9
Ratio of total rise to total run: between 6/12 and 8/9
Regardless of what you did, the ratios of step rise to step run and total rise to total run should be identical.