Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Now that we have a basic understanding of exponential functions, let’s move on to another kind of relationship. As you work through the following problems, try to get a sense of how these relationships are different from both linear and exponential functions.
“Square numbers” describe the number of dots needed to make squares like the ones below. The first square number is 1, the second is 4, and so on. Note 9
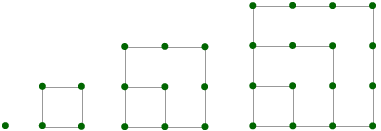
Problem C1
Draw the next two squares in this pattern. Note 10
Problem C2
Fill in the table below:
Graph the data in your table using graph paper or a spreadsheet, then describe your graph. How is it different from the linear and exponential graphs you’ve seen?
Tip: Try to be specific about how this graph is different from an exponential graph. What is the key property of an exponential graph?
Describe a rule relating the number of dots on the side of a square (the independent variable) and the total number of dots (the dependent variable).
“Triangular numbers” describe the number of dots needed to make triangles like the ones below. The first triangular number is 1, the second is 3, and so on.
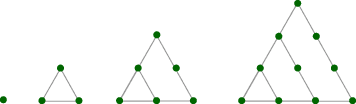
Problem C5
Draw the next two triangles in this pattern.
Problem C6
Fill in the table below:
|
Problem C7
Graph the data in your table using graph paper or a spreadsheet, then describe your graph. How is it different from the linear and exponential graphs you’ve seen?
Problem C8
Describe a rule relating the number of dots on the side of a triangle (the independent variable) and the total number of dots (the dependent variable).
Problem C9
Describe any similarities and differences between your rules and graphs for the square and triangular numbers. In a way, they both have the same kind of rule. How would you describe it? Note 11
Tip: Think about how you would go from one output to the next. What changes? Can you describe these changes with a rule?
You can create “figurate numbers” for any polygon shape. Below are pictures of the first few pentagonal and hexagonal numbers.
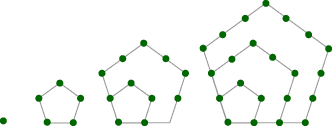
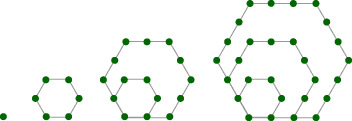
The growth of figurate numbers is an example of a quadratic function. A quadratic function’s formula will always involve squaring the input number: y = 3x2 + 5 is a quadratic function, and y = 3x + 5 is not. In Part D, we will explore the formulas and properties of quadratic functions in more detail.
Note 9
This section focuses on figurate numbers as a visual context for introducing and exploring quadratic functions. The idea is to get a sense for another kind of function without worrying too much about the details. In working through these problems, some people might come up with closed-form rules to describe the figurate numbers, and others might come up with recursive or even doubly-recursive rules (using the fact that the second differences are constant). All of these approaches make it possible to work through the problems and see how these functions are different from both the linear and exponential functions studied previously.
Note 10
Graph paper can be used to work through Problems C1-C9. If using the spreadsheet program to create the graphs, only use the data for the first six figures (or fill in the in-between entries in the table). Large jumps in inputs cause the spreadsheet graphs to distort and look less like parabolas. Since there are only a few data points for each, it might be just as easy to graph them by hand.
If you have trouble coming up with a rule for the triangular numbers, remember that the triangles you are building look a lot like the staircases built in a previous session. (In fact, the pattern is exactly the same.)
Groups: To wrap up this part, discuss how tables were filled in, particularly how missing inputs were found when given an output. Also compare rules. Some people will likely have come up with closed-form rules and others with rules like “add the previous output and the current input” (for triangular numbers). They might even have extended patterns like these:
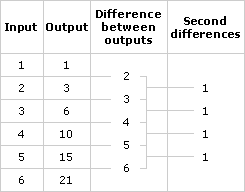
Note 11
Groups: Share thoughts on how the two graphs in this part were similar to each other and different from others they have seen. If possible, look at a picture of a parabola that includes negative inputs in order to clarify the difference in shape between a parabola and the exponential functions they saw earlier.
Problem C1
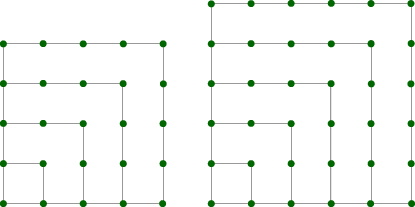
Problem C2
Here is the completed table:
|
Problem C3
It is neither a linear nor an exponential graph. Its successive outputs do not have the same ratio; therefore, it cannot be an exponential graph. It is certainly not a straight line, because successive outputs do not have the same difference, so it cannot be a linear graph.
Problem C4
The rule is O = n2, where O is the output, the total number of dots, and n is the number of dots on the side of a square. A recursive rule is Dn = Dlast + (2n – 1).
Problem C5
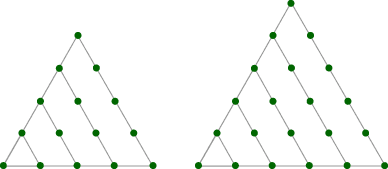
Problem C6
Here is the completed table.
|
Problem C7
As with Problem C3, the graph does not demonstrate exponential behavior, because successive terms do not have the same ratio. It’s not a linear graph, either, because it is certainly not a straight line. Actually, the graphs of the table of square numbers and the table of triangular numbers look pretty similar.
Problem C8
There is more than one answer, but one is O = (n)(n + 1) / 2. The recursive form is easier to find: Dn = Dlast + n, because n new dots are added in the nth triangle.
Problem C9
Both closed-form rules involve multiplying n by itself at some point, and both recursive rules involve adding something linear to n. Compare this to linear functions, which have only a single use of the variable in their closed-form rules, and a constant in the recursive rule.