Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In the grades 3-5 curriculum, students are frequently asked to think about patterns, but often their “pattern sniffing” skills end with simply finding the next object. Note 8
Problem E1
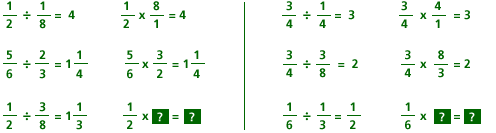
| a. | What algebraic ideas are in this lesson? |
| b. | How are patterns used in this lesson? |
| c. | What mathematics do you think students would learn from this lesson? |
| d. | Are there any misconceptions that students might develop from this lesson? |
| e. | How would you modify the problem, or what additional questions might you ask, to incorporate the framework for analyzing patterns? |
Problem E2
| a. | What algebraic ideas are in this lesson? |
| b. | How are patterns used in this lesson? |
| c. | What mathematics do you think students would learn from this lesson? |
| d. | Are there any misconceptions that students might develop from this lesson? |
| e. | How would you modify the problem, or what additional questions might you ask, to incorporate the framework for analyzing patterns? |
Note 8
In the lesson on dividing fractions, students might see a pattern of multiplying by the reciprocal. Students should, however, be asked if they understand why this method works. For this particular set of problems, this is a crucial question in their understanding of operations with fractions. Observing the pattern is not enough.
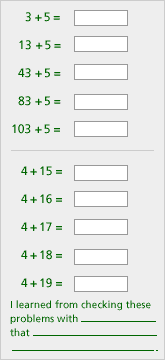
The same questions need to be asked regarding the problem from Investigations in Number, Data and Space. One of the key components in analyzing patterns is determining why they continue as they do, even “down the line.”
Problem E1
| a. | There is no algebra specifically shown in this problem. It does, however, examine some patterns. |
| b. | The patterns used in this problem compare dividing by a fraction and multiplying by its reciprocal. |
| c. | The lesson assumes that students will learn that dividing by a fraction and multiplying by its reciprocal produce the same result. |
| d. | No example shows that dividing by a whole number is the same as multiplying by its reciprocal. This could lead to confusion. There is no attempt to show why the process works. |
| e. | The lesson should include dividing by a whole number, and it should include an explanation of why the process works. |
Problem E2
| a. | There is no algebra specifically shown in this problem. It does, however, examine some patterns. |
| b. | The patterns used in this problem show two things: a) The units digit of a sum remains the same if the units digits of the addends remain the same; and b) The units digit of a sum increases by one as one addend remains the same and the other addend increases by one. |
| c. | The lesson assumes that students will learn the patterns described above. |
| d. | Students may not notice the patterns, or overgeneralize to think that all sets of problems will show similar patterns. |
| e. | The lesson should ask children to generalize and describe the patterns they see. |