Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In This Part
Problem A5 describes several different ways to extend the pattern given in Problem A1. When a sequence of numbers is not tied to a context, there is no way to determine which extension of a pattern is “correct.” Note 5
Describing patterns is most useful when the regularity is embedded in some well-understood situation. For example, examine the toothpick pattern given here:

Problem B1
Describe the pattern in as many ways as you can.
Problem B2
Imagine you keep adding triangles. Complete the following table:
| Triangles | Toothpicks |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 10 |
Problem B3
If someone tells you the number of triangles, explain how to tell them the number of toothpicks they would need. How do you know your description will always give the right number of toothpicks?
Problem B4
Use your explanation to complete this table:
| Triangles | Toothpicks |
| 2 | |
| 3 | |
| 4 | |
| 10 | |
| 100 | |
| 26 | |
| 46 | |
| 102 |
|
Video Segment In this segment, participants describe and explain different patterns they found in the toothpick triangles problem, and Professor Cossey discusses the importance of understanding where a pattern comes from. Watch the segment after you have completed the toothpick triangles problems, Problems B1-B4, and consider the different patterns that the onscreen participants identified. Do Sue-Anne and Frederick’s rules extend the table in the same way? Is there only one correct way to extend the table in Problem B2? You can find this segment on the session video, approximately 14 minutes and 10 seconds after the Annenberg Media logo. |
Problem B5
How does the table in Problem B4 compare to the table from Problem A1? Is there more than one way to extend the triangle and toothpick table? Explain.
Note 6
Table from Problem B4
| Triangles | Toothpicks |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 10 | 42 |
| 100 | 402 |
| 6 | 26 |
| 11 | 46 |
| 25 | 102 |
Table from Problem A1
| Input | Output |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 5 | 22 |
| 6 | 26 |
| ? | ? |
| ? | ? |
Problem B6
Which of the descriptions below from Problem A5 are valid for the toothpick triangles? Why are the others invalid?
Problem B7
Explain your rule for calculating the number of triangles if you are given the number of toothpicks. Why does it work?
Note 7
Problem B8
Will every number of toothpicks correspond to a number of triangles? What does this tell you about your rule?
Note 5
Look at the toothpick pattern and complete Problems B1-B8.
Groups: Work in pairs. There are two common ways of thinking about the toothpick pattern, and one of the reasons it’s useful to work in pairs or small groups is to observe this variety.
Some people see the pattern as groups of 4 toothpicks, with 2 toothpicks added on to the right-most triangle, and they come up with the following rule: Take the number of triangles, multiply by 4, and add 2. Others see the pattern as groups of 6 toothpicks, with 2 toothpicks removed from all of the triangles except the right-most triangle. The rule they come up with is: Take the number of triangles, multiply by 6, and then subtract 2 times 1 less than the number of triangles.
When using a variable, the first rule turns out to be 4n + 2; the second becomes 6n – 2(n-1). The second rule may be harder to represent,”subtract 2 times 1 less than the number of triangles” can be tricky to express. Consider going through a derivation of this rule, starting with: If the number of triangles is 5, what’s 1 less? So we subtract 2 times that. If the number of triangles is 10, what’s 1 less? Then subtract 2 times that number. Finally, if the number of triangles is n, what’s 1 less? It is n – 1.
The second difficulty may be seeing the need for the parentheses when multiplying this quantity by 2. Explore the expressions 2(n – 1) and 2n – 1, testing some particular values for n to decide which accurately describes “2 times 1 less than n.”
Those who come up with a symbolic rule right away, without even looking at the drawing, should think about where the “4-ness” or the “6-ness” comes from in the picture. Make sure to make the link between what’s going on in the equation and what’s happening in the picture.
Groups: No matter how people come up with them, explore the two different rules as a full group. Do they continue the table in the same way? Are the rules equivalent, even though they look different? Or are they genuinely different?
Note 6
Groups: Go over Problem B5 as a full group.
In this situation there is only one way to fill in the table because the data is linked to a situation. Whatever the number of triangles, we can visualize how many toothpicks are needed.
Note 7
Be sure to go over Problem B7. Here, we are given the number of toothpicks and are asked to work backwards to find the number of triangles. Working backwards is a hallmark of algebraic thinking; we will revisit this idea in a later session.
Problem B1
Some possible descriptions:
Problem B2
Here’s the completed table:
| Input | Output |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 10 | 42 |
Look familiar? It should — it’s the table from Problem A1.
Problem B3
The number of toothpicks is 4 times the number of triangles, plus 2. Look at what happens when each new shape is built. Specifically, imagine that you have the shape for 1 triangle already built, and you need to build the shape for 2 triangles. You would only need to add 4 toothpicks to the left of the existing shape. Sure enough, these 4 are what you’d need to build the 3rd shape on to the 2nd, and so on. So each new triangle means 4 new toothpicks. The “+ 2” comes from the lower right corner of the original triangle, which is not part of the shape added on each time.
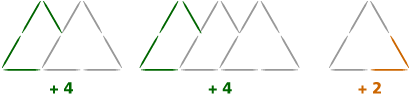
You can be sure that the description always gives the correct number of toothpicks because there is a specific context to the problem. The method of creating new triangles never changes, so you can be sure that each triangle will have 4 more toothpicks than the last. Compare this to Problem A5; without a context, there is no guaranteed pattern.
Problem B4
Some predictions:
| Triangles | Toothpicks |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 10 | 42 |
| 100 | 402 |
| 6 | 26 |
| 11 | 46 |
| 25 | 102 |
Problem B5
One subtle change between this table and the table in Part A is that we can be sure the pattern in this table will continue as long as necessary.
Problem B6
Patterns like the ones listed in parts (f) and (g) in Problem A5 will not happen in this context. The others (parts (a) through (e)) are valid.
Problem B7
One way to calculate the number of triangles is to “undo” the way we turn triangles into toothpicks. To get toothpicks from triangles, we multiply by 4, then add 2. So to “undo” these operations, we have to subtract 2, then divide by 4. So the number of triangles can be determined by this process, or it can be determined by the rule n = (T – 2) / 4.
Problem B8
No. For example, there would never be a number of triangles for 1004 toothpicks. This means that the rule developed in Problem B7 only works for numbers that produce a positive whole number as the output.