Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Algebraic Structure Homework
Session 9, Homework
Problems
Problem H1
In this game, starting with a string of Ys and Zs, the object is to simplify the string by following strict rules. The rules are:
| • | YYY can be erased. |
| • | ZZ can be erased. |
| • | The commutative law holds: YZ = ZY. |
| • | E is the empty string (a string with no Ys or Zs). |
|
|||||||||||||||||||||||||||||||
Simplify the following strings:
| a. | YZYZZYYZ |
| b. | YYYYZZYZY |
| c. | YZYZYZYZYZYZYZYZZZYZYZYYZY |
Problem H2
Including the empty string E, there are six essentially different strings that cannot be simplified. They are called the elements of the YZ group.
Find all the elements of the YZ group.
Problem H3
The symbol “*” represents the operation “put together and simplify.” For example:
| • | YZ * YZ = YY |
| • | Y * E = Y |
Compute:
| a. | E * YZ |
| b. | YZ * YY |
| c. | Z * YZ |
Problem H4
Find the missing term.
| a. | YZ * __ = E |
| b. | Z * __ = YZ |
| c. | YY * __ = Z |
Problem H5
For the YZ group, * works a little bit like multiplication. Another way to write the first two rules is Y3 = E and Z2 = E. Explain.
Problem H6
The only powers of Y are Y, Y2, and E. Explain.
Problem H7
Find all the powers of each element of the YZ group.
Problem H8
Simplify:
| a. | Y1,000 |
| b. | (YZ) 1,001 |
Problem H9
Make a * table.
Problem H10
What element of the group works like the number 1 for multiplication?
Problem H11
What is the reciprocal of each element?
Homework problems are adapted from Algebra: Themes, Tools and Concepts, by Anita Wah and Henry Picciotto (New York: Creative Publication, Wright Group/McGraw-Hill, 1993), p. 159. The above materials may not be reproduced without the written permission of Wright Group/McGraw-Hill.
The above materials may not be reproduced without the written permission of Wright Group/McGraw-Hill.
Solutions
Problem H1
a:
|
b:
|
c:
|
Problem H2
The elements of the YZ group are E, Y, YY, Z, YZ, and YYZ.
Problem H3
Y3 means the same as Y * Y * Y, which is YYY, which is the same as E. The same is true of Z2, which is identical to Z * Z.
Problem H4
Y3 means the same as Y * Y * Y, which is YYY, which is the same as E. The same is true of Z2, which is identical to Z * Z.
Problem H5
Y3 means the same as Y * Y * Y, which is YYY, which is the same as E. The same is true of Z2, which is identical to Z * Z.
Problem H6
Since Y3 is identical to E, Y4 will be identical to Y, Y5 = YY, Y6 = E, etc.
Problem H7
Powers of each element:
| • | E: E only |
| • | Y: Y1 = Y, Y2 = YY, Y3 = E |
| • | YY: YY1 = YY, YY2 = Y, Y3 = E |
| • | Z: Z1 = Z, Z2 = E |
| • | YZ: YZ1 = YZ, YZ2 = YY, YZ3 = Z, YZ4 = Y, YZ5 = YYZ, YZ6 = E |
| • | YYZ: YYZ1 = YYZ, YYZ2 = Y, YYZ3 = Z, YYZ4 = YY, YYZ5 = YZ, YYZ6 = E |
Problem H8
| a. | Y1,000 = Y1, since 1,000 = 1 (mod 3), and the powers of Y repeat every three powers. |
| b. | (YZ)1,001 = (YZ)5, since 1,001 = 5 (mod 6), and the powers of YZ repeat every six powers. According to the list of powers of YZ, (YZ)5 = YYZ. Another way to do this is to imagine a line of 1,001 Ys and 1,001 Zs, and decide what would be left after all the cancellation. |
Problem H9
Here is the completed table:
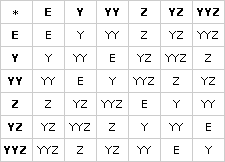
Note that every element appears exactly once in each row, and once in each column.
Problem H10
The element E works this way, since E * A = A for any element A in the table, just like 1 * N = N for any number N.
Problem H11
The reciprocals can be found by finding E within the row and column of each element. Here are the reciprocals, in pairs:
| • | E and E |
| • | Y and YY |
| • | Z and Z |
| • | YZ and YYZ |
