Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
More Nonlinear Functions Part B: Inverse Proportions (60 minutes)
Session 8, Part B
In This Part
- Splitting a Prize
- Ms. Anwar’s Backyard
- Another Inverse Proportion
Splitting a Prize
Imagine that the teachers in your school decide to play the lottery together. If they win, the prize is $800,000. Problem B1 is a table that shows how much each teacher will get, depending on how many of them contribute to buy the tickets. Note 4
Problem B1
Fill in the rest of this table: Note 5
Problem B2
Describe a rule that fits the table. Try to find more than one rule. Explain why your rule will work if the table is continued.
Problem B3
Graph the rule that shows how much each teacher will receive. Describe how this graph is different from other functions you’ve seen.
Tip: Make sure you distinguish this function from all the other functions you’ve seen — linear, exponential, quadratic, and cyclic.
|
Video Segment What would a value of y = 0 mean in terms of the lottery problem? There is an important difference between this type of function — a decreasing curve — and a decreasing line. You can find this segment on the session video, approximately 10 minutes and 15 seconds after the Annenberg Media logo. |
Functions like this are called inverse proportions. The relationship between the two variables in this function is called inverse variation. Inverse proportions are another example of nonlinear functions.
You can think of inverse proportions in two ways:
- output = some constant / input, or
- input * output = some constant
There are many applications of these kinds of functions. If you’re getting paid a fixed amount of money to do a job, for example, your hourly rate depends on how quickly you complete the work. The shorter the time, the larger the hourly rate.
Ms. Anwar's Backyard
Ms. Anwar is considering renting a house that has a large rectangular backyard. She wants to figure out if there will be room for her children’s play equipment. The owner told her, “The backyard has an area of 2,000 square feet.” Ms. Anwar thought about what he said and tried to imagine what the actual dimensions of the yard might be.
Problem B4
Fill in the table below to show some possibilities for the dimensions of the yard if the area is 2,000 square feet.
| Length | Width | Area = length * width | ||
| 50 | 40 | 2000 | ||
| 25 | 2000 | |||
| 100 | 2000 | |||
| 2 | 2000 | |||
| 2000 | ||||
| 2000 | ||||
| 2000 | ||||
| 2000 |
Problem B5
Find an equation relating the length (x) and the width (y) in the table above.
Problem B6
Graph the length vs. width in the table above.
Problem B7
As x changes, what happens to y? Try to describe this relationship as clearly as possible. These problems may help you:
Note 6
- Complete the table below. Round values for y to one decimal place, or use the exact fractional value.
x y Decrease
in y20 100 — 30 66.7 33.3 40 50 60 70 80 90 100 - As x increases by 10, what happens to y? Does y go up a fixed amount? An increasing amount? A decreasing amount?
- As x doubles, what happens to y? As x triples, what happens to y?
- If x is very small, what can you say about y? What if x is very big?
“Ms. Anwar’s Backyard” problem taken from IMPACT Mathematics Course 3, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p.110. www.glencoe.com/sec/math
Another Inverse Proportion
Consider a new function: (x)(y) = 3. Answer these questions:
Problem B8
Find five negative and five positive x values between -10 and 10. Record them in a table with the corresponding y-values. Be creative! Try some non-integers.
Tip: Values like 1/2 and 1/10, -1/2 and -1/10 are interesting to try
Problem B9
If x = 0, what happens to y? What happens on a calculator if you ask for the value of y = 3 / x when x = 0?
Problem B10
Create a graph of this function. What happens as the graph gets near the y-axis? Will it ever cross the y-axis?
Tip: Make sure this graph includes points where x is positive, and other points where x is negative. See Problem B8 if you’re unsure what will happen if x = 0.
Take It Further
Problem B11
In the equation (x)(y) = 3, what does the 3 represent, graphically?
Tip: Looking back at the Interactive Activity may help.
Problem B12
You’ve seen two kinds of functions that have similar names: proportion (or direct variation) and inverse proportion (or inverse variation). Compare and contrast these two functions. What does the word “inverse” indicate in this case? Note 7
Take It Further
Problem B13
The equation (x)(y) = 1 is a special kind of inverse variation. How are x and y related in this equation? What does this relationship have to do with solving equations?
Problems B8-B10 adapted from IMPACT Mathematics Course 3, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p. 111.
Notes
Note 4
The two ways to think of inverse proportions are as input * output = constant and as output = constant / input. Both are useful for different situations.
Note 5
Groups: Work through Problems B1-B3, and then discuss the terms “inverse proportion” and “inverse variation.” Move on to Problems B4-B12. Discuss these problems as a group, especially how inverse proportions are different from other functions we’ve seen.
Unlike other functions we’ve seen, increasing the input (in magnitude) decreases the output by the same factor (in magnitude). As long as the numerator is positive, as x gets bigger, y gets smaller. This is a striking difference from other functions.
Note 6
Groups: Discuss Problem B6, particularly what’s going on in the table. Some observations that may arise are, “As x increases, y decreases, but by less and less each time.” Or, “As y decreases, so does the amount by which it decreases.” Or, “As y gets smaller, it does so at a slower and slower rate.”
It’s also important to think about the graph and whether it will cross either of the axes. Going back to the contexts of the problems (sharing money among several people, for example) should help make sense of the asymptotic nature of the graphs.
Note 7
Groups: Take 10 minutes to jot down answers to Problems B11 and B12, then share answers.
Take time to think about the how the word “reciprocal” describes the relationship (x) (y) = 1. There are some important and often confused ideas here. For example, 1 has a reciprocal (itself). The fraction 1/5 also has a reciprocal: 5. Too often, students and teachers think of whole numbers as the “regular” numbers and the “reciprocals” as 1/n. Reciprocals can be used in solving equations. When you solve 3x = 9 by “dividing each side by 3,” another description is “multiplying each side by the reciprocal of 3.” This method generalizes to other systems (equations involving matrices or equations involving modular systems, which we will see in Session 9), whereas the “divide by 3” method is specific to the real numbers.
Groups: End this part by adding inverse proportions to the list of functions.
Solutions
Problem B1
Here is the completed table:
|
The last two entries will vary.
Problem B2
One rule is that the product of the input and the output is always 800,000. If M = the money each teacher receives, and T = the number of teachers, then
(M) x (T) = 800,000. This is because the total prize of 800,000 is split evenly among the teachers. This also leads to a second rule: M = 800,000 / T, because the money received by each teacher is 800,000 divided by how many teachers split the prize. Additionally, T = 800,000 / M.
Problem B3
The amount of money decreases as the number of teachers increases, but it is not an exponential decay because the ratio between consecutive outputs is not constant. Looking at differences between outputs guarantees that the graph is neither linear nor quadratic. The graph is not cyclic, because there is no point where the outputs begin to repeat.
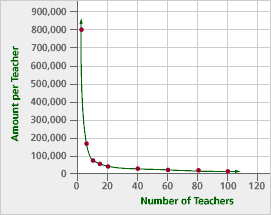
Problem B4
Here is the completed table:
|
||||||||||||||||||||||||||||||||||||||||||||||||||
The last four entries will vary.
Problem B5
One equation is x * y = 2,000. Note that Area = length * width is always constant at 2,000. Other possible equations are y = 2,000 / x and x = 2,000 / y.
Problem B6
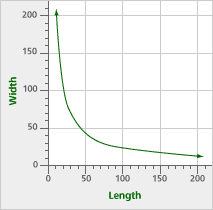
Problem B7
Overall, if x is multiplied by a number, y is divided by the same number. If x is divided by a number, y is multiplied by the same number.
-
- Here is the completed table. All y-values are rounded to one decimal place.
x y Decrease in y 20 100 — 30 66.7 33.3 40 50 16.7 50 40 10 60 33.3 6.7 70 28.6 4.7 80 25 3.6 90 22.2 2.8 100 20 2.2 - As x increases by 10, y continuously decreases, but the rate of decrease lessens as x grows.
- If x doubles, y is cut in half. If x triples, y is divided by three.
- If x is very small, y must be very large, since the product of x and y is always the same. By the same argument, if x is very large, then y must be very small.
- Here is the completed table. All y-values are rounded to one decimal place.
Problem B8
Let’s try it:
|
|||||||||||||||||||||||||||||||||||||||
Problem B9
If x = 0, y is undefined, which means that no value of y will make zero times y equal to 3. Using a calculator, 3 / 0 will fail to return a number; the calculator will give an error message.
Problem B10
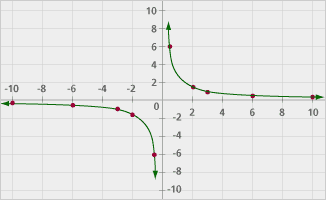
The graph will not cross the y-axis, because if it did, it would mean that some y-value would be assigned for x = 0 for the graph, and, as explained in the solution to Problem B9, there is no such value. Another way to look at it is to examine the behavior of the graph near x = 0. If x is a little more than zero, y is a very large, positive number, but if x is a little less than zero, y is a very large, negative number. These portions of the graph do not meet.
Problem B11
The 3 represents the area of a rectangle drawn with (0, 0) as one corner and any point on the graph as the opposite corner. Compare this to the Interactive Activity, where there were rectangles of area equaling 2,000 feet — length times width always equaled 2,000. Here, x is the length, and y is the width.
Problem B12
In a direct variation function, an increase in x creates a proportional increase in y; if x is multiplied by 5, y is also multiplied by 5. But in inverse variation, the opposite is true: If x is multiplied by 5, y is divided by 5. The word “inverse” refers to the inverse operations of multiplication and division.
Problem B13
In this particular equation, x is the reciprocal of y, because x and y multiply together to make 1. The reciprocal is used to solve equations like 5n = 16 — multiplying both sides of the equation by the reciprocal of 5 produces two numbers (5 and 1/5) which, when multiplied, make 1. So, multiplying by 1/5 will remove the 5 from the left side, leaving variable n by itself. This is the key to solving equations by backtracking.
