Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Patterns in Context Part C: Different Uses of Variables (25 minutes)
Session 2, Part C
In the toothpick problem, we used a variable to describe the relationship between the number of toothpicks and the number of triangles in the pattern. The use of variables is the most familiar part of working algebraically. We have also seen in the Eric the Sheep problem that algebraic thinking does not always require using variables. The concept of variable, however, is an important one in algebra. In fact, there are many meanings for variables and how they are used in mathematics.
Note 8
Mathematician Zal Usiskin has outlined four conceptions of algebra based on different uses of variable:
Conception 1: Algebra as generalized arithmetic. Here, variables are indeterminates— they do not have specific values, but allow you to analyze operations like multiplication and addition.
Example: The sum of 2 even numbers is even: 2a + 2b = 2(a + b).
Example: Any number times zero is zero: 0 x n = 0
Conception 2: Algebra as a study of procedures for solving certain kinds of problems. Here, the variables are unknowns, and you want to solve for them.
Example: When 4 is added to 9 times a certain number, the sum is 40. Find the number. We represent this as 4 + 9n = 40, and n is the unknownsolution.
Example: You get paid $10 per hour and earned $30 in tips. In total, you made $380 last week. How many hours did you work? Here, the unknownis the number of hours worked.
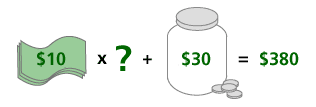
Conception 3: Algebra as the study of relationships among quantities. Here the variables really vary, and you look at how changes in one variable affect the others.
Example: In a rectangle, area is length times width: A = L x W.
Example: What happens to the value of 1/x as x gets larger and larger?
Example: In Part B, what happens to the number of toothpicks as the number of triangles increases?
Conception 4: Algebra as the study of structures. This conception of algebra explores the nature of numbers and operations, and we will explore this conception in greater detail in Session 9.
It is clear from these descriptions that variables can be used in different ways and for different purposes. The relative importance given to these multiple uses of variables affects the purposes for which algebra is used as well.
Problem C1
Come up with at least two other examples of “generalized arithmetic.” Write your examples in words, symbols, or both. Note 9
Problem C2
Think of as many ways as you can to solve the equation 4 + 9n = 40; that is, to find a number so that 4 added to 9 times that number is 40.
Problem C3
Describe at least two other situations where variables represent relationships between quantities.
Notes
Note 8
We’ve been using variables to describe patterns concisely, and some would claim that this is a move toward algebra. But what is algebra?
Groups: Discuss this question in small groups, then share answers with the whole group.
Reflect on this statement from mathematician Zal Usiskin that describes what algebra is: “Algebra is not easily defined.” In the first session, we clearly used algebraic thinking to describe the pattern in the Eric the Sheep problem, but we didn’t use an equation with variables. When we focus on the concept of variable, we can see that variables have many facets, as illustrated in the following examples:
- A = LW
- 40 = 5x
- sin x = cos x * tan x
- 1 = n * (1/n)
- y = kx
Each of these has a different feel. Can you explain the differences?
If you get stuck, here’s a way to sort through these examples:
- Example 1 is a formula.
- Example 2 is an equation or open sentence to solve.
- Example 3 is an identity that is true for any value of x, other than when cos x = 0.
- Example 4 is a property that is true for all n not equal to 0.
- Example 5 is an equation representing a direct variation function, where it is implied that k is a constant and y and x are variables.
Each of these has a purpose in the study of algebra, and to quote again from Usiskin:
“Purposes for algebra are determined by, or are related to, different conceptions of algebra, which correlate with the different relative importance given to various uses of variables.”
Also, consider this quote by Bob Davis: “Algebra is the way we talk about what numbers do when we don’t know what the numbers are. ”
Now go on to Usiskin’s four conceptions of algebra. Read through the conceptions as described in the course materials.
Groups: Discuss the first three conceptions (saving the fourth for the last session) and the examples contained in the descriptions. Group members can help each other understand the different representations in the examples — for instance, the representation of “even numbers” as “2a” and “2b.”
Note 9
Groups: Work in small groups on Problems C1-C3. Spend some time sharing responses. Some people may need help in using symbols to describe their work to explain what the symbols are showing.
Solutions
Problem C1
Generalized arithmetic allows you to state things like the commutative property of addition: a + b = b + a. Or the property that when you add zero to a number, you get the same number: 0 + n = n. Or the property that the product of two square numbers is a square number: x2 * y2 = (x * y)2.
Problem C2
The answer is n = 4. One method is the patented “guess-and-check.” Others include systematic testing of values of n starting with n = 1, or “undoing” the operations on the left side – if we have to multiply n by 9, then add 4, a way to find n would be to subtract 4, then divide by 9.
Problem C3
Some situations include the relationship between the length of a side of a square and the square’s area (A = s2), the relationship between Fahrenheit and Celsius temperature (F = 1.8C + 32), and the relationship between distance, rate, and time (D = r * t). In all of these, the variables vary and represent relationships between two or more quantities.
