Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
The National Council of Teachers of Mathematics’ Principles and Standards for School Mathematics (2000) identifies algebra as a strand for grades Pre-K-12. The Standards identify the following concepts that all students should cover and be able to:
Note 4
| • | Understand patterns, relationships, and functions |
| • | Represent and analyze mathematical situations and structures using algebraic symbols |
| • | Use mathematical models to represent and understand quantitative relationships |
| • | Analyze change in various contexts |
For the Pre-K-2 classroom, understanding patterns includes the following expectations:
| • | Recognize, describe, and extend patterns such as sequences of sounds and shapes or simple numeric patterns, and translate from one representation to another |
| • | Analyze how repeating and growing patterns are both generated |
In this part, we’ll look at problems that foster algebraic thinking as it relates to these standards, and we’ll explore ways of asking questions that elicit algebraic thinking. The situations you will be exploring are representative of the kinds of problems you would find in some existing texts; in fact, you may recognize some of them! The goal is for you to examine these problems with the critical eye of someone who has taken this course and is beginning to view algebraic thinking with a different perspective.
Consider the situation below, appropriate for exploration in a K-2 classroom:
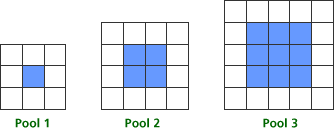
Tat Ming is designing square swimming pools. Each pool has a square center that is the area of the water. Tat Ming uses blue tiles to represent the water. Around each pool there is a border of white tiles. Here are pictures of the three smallest square pools that he can design, with blue tiles for the interior and white tiles for the border.
Note 5
Problem B1
What questions would you, as an adult mathematics learner, want to ask about this situation?
Problem B2
How do your questions reflect the algebra content in the situation?
Now focus on the questions you want the students in your classroom to consider. In kindergarten, begin by having students focus on the relationship between the numbers of blue and white tiles by sorting the tiles into blue tiles for the water and white tiles for the border. In a first-grade class, students might focus on the blue tiles and what it means to be square. In a second-grade class, students might begin to organize their data into a table.
Problem B3
What patterns, conjectures, and questions will your students find as they work with this situation?
Problem B4
What questions could you as the teacher pose to elicit and extend student thinking at your grade level?
Problem B5
Recall the framework you explored in Session 2 in looking at patterns: finding, describing, explaining, and using patterns to predict. Which of these skills will your students use in approaching this problem?
Problem B6
Read the article “Experiences with Patterning” from Teaching Children Mathematics. What ideas mentioned seem appropriate for your classroom?
Here’s a problem on patterns developed for a kindergarten class:
Shoe Patterns
Focus: Extend patterns
Materials: Children’s shoes
Children sit in a circle, and each child removes one shoe. Arrange some of the shoes in a patterned line. (For example, the pattern might be: vertical, horizontal, vertical, horizontal; this is a nice opportunity to use these terms). Ask if children think they know how to add their shoes to the line, following the pattern. Let several children add their shoes to either end of the line before you ask them whether they can describe the pattern. Let the rest of the children add their shoes and see how far the pattern reaches.

Problem B7
What questions could you ask to develop students’ skills in describing patterns?
Problem B8
What questions could you ask to develop students’ skills in predicting?
Note 4
Look at NCTM’s recommendations for content in the algebra strand in the Standards,then look at the problem for designing square swimming pools. After reading the problem, work on Problems B1-B5.
Note 5
Read the commentary on the swimming pool problem in “Experiences with Patterning,” by Joan Ferrini-Mundy, Glenda Lappan, and Elizabeth Phillips, in Teaching Children Mathematics (February 1997), p. 282-288.
Download PDF File:
Problem B1
Answers will vary. One question might ask how to use the pictures to help find the relationship between the pool number and the numbers of white and blue tiles.
Problem B2
Answers will vary. For the question above, you might discuss building each pool. For example, the blue part of Pool 1 is a 1-by-1 square and takes one blue tile, the blue part of Pool 2 is a 2-by-2 square and takes four blue tiles, etc.
Problem B3
Answers will vary. At this level, many students will see that the blue tiles are always in the shape of a square, and that there are always an even number of white tiles. Some may recognize that the number of white tiles is always a multiple of four.
Problem B4
Answers will vary. At this level, teachers should encourage students to describe the shape of the blue tiles. Ask students to tell you how to build the blue part of Pool 4. Then ask them to think about putting white tiles around that blue pool. How many white tiles do you need for the top? How many for the bottom? Now think about putting tiles around the sides.
Problem B5
Answers will vary. At this level, students should actually build the pools with two different color square tiles, then describe what they built. The process of building will help students put the patterns into words. Many students will use all these skills when solving this problem. For students that are having difficulty, build only the blue part first.
Problem B6
Answers will vary. All of the ideas described in the K-2 section are appropriate for this level student. Many students at this level will be able to answer questions posed the Grades 3-5 section.
Problem B7
Answers will vary. Ask students to describe the directions that the toes of the shoes face, using words like up and left.
Problem B8
Answers will vary. Ask students to repeat the pattern with you by saying: Up, left, up, left, up, left, up, … . Now ask them to continue the pattern.