Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Solving Equations Homework
Session 6, Homework
In the puzzles that follow, each shape stands for a number value of “weight.” To solve these puzzles, make the weights in each part of the mobile balance from left to right, just as a sculptor might balance all the parts of a mobile. Here are the rules:
- The right and left sides of each horizontal beam must balance.
- Each shape has a unique and consistent weight within a puzzle, and no shapes weigh 0.
- Take the clues at face value. For example, if a clue says that the square’s weight is a multiple of the triangle’s weight, you can assume that the triangle does not weigh 1.
- All weights are either one- or two-digit, positive whole numbers.
- A piece hanging directly below the fulcrum does not affect the balance between the left and right arms. Although this piece has its own definite weight, it remains “neutral” for the purpose of balancing the other two arms.
- The size of the pieces has no relation to weight.
- These mobiles are exercises in balancing number values. They do not take into account the distance from the fulcrum.
Tip: Think about the total weight of each branch of the mobile, which may give you the values of certain weights or help you find equations relating weights. In tougher puzzles, make a list of possible values for a weight, then try to reduce that list to one correct value. Problem H4 is a system of equations with eight variables, and is very difficult.
Problem H1
Discover the value of each of the shapes. The total weight is 36. All shapes weigh less than 10.
Problem H2
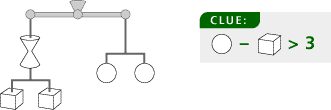
Discover the value of each of the shapes. The total weight is 80. Only one shape weighs more than 9.
Problem H3
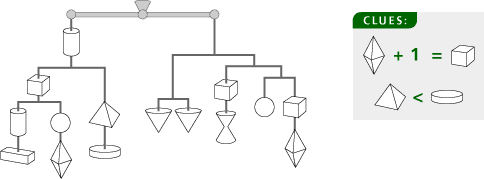
Discover the value of each of the shapes. The total weight is 54. The three arms are equal in weight.
Problem H4
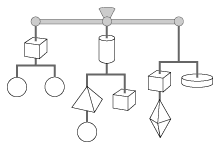
Discover the value of each of the shapes. The total weight is 180. Each of the three arms is equal in weight.
Problem H5
Marcus had some cookies. He wanted to give them all away. He gave one half of them to his friend David. They divided the remaining cookies evenly among David’s three brothers, so each got 4. How many cookies did Marcus have originally?
Tip: Which of the methods of solving equations that you have learned in this session can be useful here? There is more than one answer.
Balance problems excerpted from In the Balance, by Lou Kroner (New York: Creative Publications, Wright Group/McGraw-Hill, 2000).
The above materials may not be reproduced without written permission of Creative Publications.
Suggested Reading
Stacey, Kaye. “Ideas about Symbolism That Students Bring to Algebra.”
Reproduced with permission from The Mathematics Teacher, © 1997 by the National Council of Teachers of Mathematics. All rights reserved.
Solutions
Problem H1
The circles must each be 9, because the mobile splits twice. The clue tells us the cubes cannot weigh more than 5 each. Because the hourglass and 2 cubes weigh 18 and the hourglass weighs less than 10, each cube is 5 and the hourglass is 8.
Problem H2
The upside-down cone is 10 (2 splits), and the circle is 5 (3 splits). Because the cube and the diamond make 5 together, the clue tells us the diamond is 2, and the cube is 3. The others: hourglass = 7, cylinder = 6, horizontal bar = 1, pyramid = 8, flat disk = 9.
Problem H3
The flat disk must be 9 (2 splits). The cube must be an even number, and larger than the circle — this makes it 8. The others: circle = 5, pyramid = 3, cylinder = 2, diamond = 1.
Problem H4
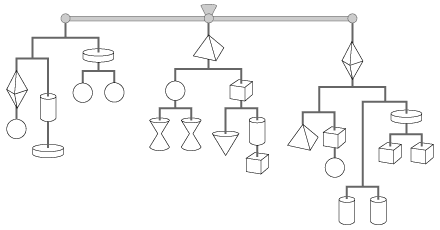
One possible course is to find the value of the diamond first. After the diamond in the third set, there are three consecutive splits (to the cylinders), so the total weight after the diamond must be a multiple of 8. This limits the possible values of the diamond shape to 4 or 12, because the diamond on the left, when paired with a circle, weighs a total of 15. Investigating the circles in the left branch shows that the circle must be 11, and the diamond must be 4. The others: cylinder = 7, flat disk = 8, pyramid = 14, hourglass = 6, cube = 3, upside-down cone = 10.
Problem H5
Backtrack or work from false position.
Backtracking: Each brother got 4 cookies, so the brothers shared 12. This is half of the original number of cookies, so the original number is 24 (multiply 12 by 2).
False position: Pick a convenient number of cookies for Marcus, then see what would have happened. Say that Marcus had 60 cookies (a good number, since 60 is very divisible). Half go to David, so there are 30 to split among 3 brothers. If Marcus had 60, each brother gets 10 cookies.
So, to turn 10 into 4 we need to multiply by 0.4, which shows that Marcus had (60)(0.4) = 24 cookies to start.
As with Problem B10, finding the solution by covering up is possible, but difficult. A solution found by doing the same thing to both sides is only possible after creating an equation for the entire situation.
