Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In This Part:
Mathematicians have always been interested in solving equations. Over the past 150 years they have studied techniques for solving equations, properties of operations that allow one to develop strategies for solving equations, and, eventually, entire systems in which one can calculate, and hence solve, equations. Note 4
These algebraic structures have become the primary focus of modern algebra. An algebraic structure is a collection of objects and operations that can be used to calculate and solve equations. The objects can be numbers, polynomials, geometric figures, points in space, card shuffles, or just about any mathematical object you can think of. The operations are usually binary operations, operations that combine two objects and form another of the same type.
Examples of systems include the system of integers and the system of rational (whole and fractional) numbers. Here, the operations are the usual operations of arithmetic — addition, multiplication, etc. The structural approach to algebra has enormously widened the kinds of systems in which algebraists work, and hence has changed the face of what’s considered “algebra.”
Algebraic structures come up naturally in mathematical investigations. In Part C, we will investigate units digit arithmetic. Our goal here is to look at the underlying structure of this arithmetic, not just the calculations involved in it. Suppose, for example, that you are looking at the last digit, or units digit, of whole numbers. (Note: In Parts C and D of this session, an “*” is used to represent multiplication.)
Find the units digit of:
(22 * 43 + 59 * 27) * (47 + 1,432 * 268 * 21,343)
One way to do this is to carry out the entire calculation and then to look at the units digit. But there’s no need for that much work; you can predict what the units digit will be without making the explicit calculations. For example, the units digit of 22 * 43 will be 2 * 3 = 6. And the units digit of 59 * 27 will be the units digit of 9 * 7 (that is, 3), so (22 * 43 + 59 * 27) will have the same units digit as 6 + 3. In other words, you can replace the numbers in the calculation by their units digits, turning the very large problem into a more manageable one:
(2 * 3 + 9 * 7) * (7 + 2 * 8 * 3)
Then, you can simplify as you go, so that, for example, (2 * 3 + 9 * 7) becomes 6 + 3, which becomes 9. These calculations depend upon order of operations. Look at the tip in Problem C1 below if you are unfamiliar with this concept.
Problem C1
Using this line of reasoning, find the units digit of 2,314 * 426 + 573 * 234.
Note 5
Tip: The order of operations — which operations you do first, second, and so on — are: inner parentheses, exponents, multiplication or division, addition or subtraction.
Problem C2
True or false: The units digit of 2,314 * 426 + 573 * 234 is the same as that of 2312 x 422+ 576 x 232.
Tip: Try to answer this question by doing as little calculation as possible.
Problem C3
Find the units digit of
(312 * 423 + 57 * 57) * (28 + 1,045 * 68 * 68 * 68)
Video Segment
In this video segment, Prof. Cossey asks participants to find the units digit of the product in Problem C3 above. Try Problem C3 yourself, then compare your work to that of the onscreen participants.
What shortcuts did you use while working on Problem C3? Can these shortcuts always be used in this algebraic structure?
You can find this segment on the session video, approximately 5 minutes and 21 seconds after the Annenberg Media logo.
Problem C4: Write and Reflect
Some people say that “the units digit of the sum is the units digit of the sum of the units digits” and “the units digit of the product is the units digit of the product of the units digits.” Explain what they mean. Is what they say correct? Why or why not?
The kind of reasoning you are doing in Problem C4 is one which begins to address the structure of units digit arithmetic.
Take It Further: Problem C5
Explain why “taking the units digit” is the same as “divide by 10 and take the remainder.”
The fact that these are the same explains why “taking the units digit” is a modular arithmetic.
What we have been exploring is a “units digit arithmetic,” an arithmetic whose objects are the digits 0 through 9, and whose operations are “add and take the units digit” and “multiply and take the units digit.” The whole system can be captured in two tables (with some of the results left blank for you to complete later):

These tables define an algebraic structure on the set of numbers
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
You can forget that these tables came from “taking the units digit” and concentrate on the system they describe. There are sophisticated words for this process of “ignoring where it came from and concentrating on the behavior” like “abstraction” and “decontextualization.” These are useful mathematical habits of mind. In some situations, you want to forget the meanings of these operations and just work with them. In other situations, it’s just as important to be able to go back to the source of these things (to “contextualize” them) and to remember that these tables came from looking at units digits or remainders. Note 6
In some of the following problems, you can work with the tables without worrying where the operations come from. In others, especially when you need to think about why a property you see in the table holds, you’ll need to go back to the context (taking units digits or taking remainders on division by 10). This fluctuation in and out of contexts is typical of the way mathematics is performed.
Problem C6
Fill in the missing entries in each table. As you complete the tables, look for patterns in the numbers you enter.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
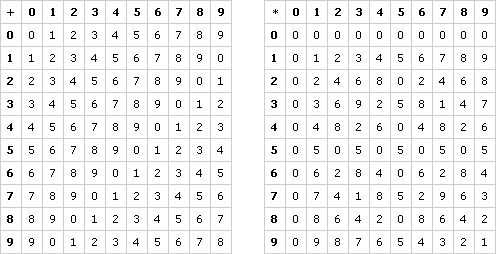
Problem C7
Does order count in addition? How can you tell just by looking at the “shape” of the + table?
Tip: How is the location of 5 + 8 related to the location of 8 + 5 in the table?
Problem C8
Go back to the context (units digits or remainders by 10) and explain your answer to Problem C7.
Problems C7 and C8 show that this algebraic structure is commutative under addition; that is, the order of the object being added does not matter.
Problem C9
Does order count in multiplication? How can you tell just by looking at the “shape” of the * table?
Problem C10
Go back to the context (units digits or remainders by 10) and explain your answer to Problem C9.
Problems C9 and C10 show that this structure is commutative under multiplication; that is, the order of the objects being multiplied does not matter.
Problem C11
Is it true of this new addition that adding 0 doesn’t change a number? Explain.
Since 0 does not change a number under addition, it is the identity element of this structure; that is, adding zero to a number does not change the value of that number.
The opposite or negative of a number is the number you have to add to it to get 0. In ordinary arithmetic, the opposite of 4 is -4 (think of a thermometer). In ordinary arithmetic, every number has a negative (what’s the negative of 0?). In our little algebraic structure above, units arithmetic, the opposite of 4 is 6, because 4 + 6 = 0.
Problem C12
Does every number have an opposite in this system? Explain.
Tip: You can use the addition table above to find opposites.
Under addition, 4 and 6 are additive inverses, because 4 + 6 = 0. Numbers which are inverses under addition are more typically referred to as opposites.
Problem C13
Give a rule for determining the opposite of a number, if it has one.
Video Segment
This short video segment describes how to find opposites using the table of addition in mod 10.
You can find this segment on the session video, approximately 13 minutes and 43 seconds after the Annenberg Media logo.

Problem C14
Is it true of this new multiplication that multiplying by 1 doesn’t change a number? Explain.
Under multiplication, 3 and 7 are inverses, because 3 * 7 = 1. Numbers which are inverses under multiplication are more typically referred to as reciprocals. The reciprocalof a number is the number you have to multiply it by to get 1. In ordinary arithmetic, the reciprocal of 3 is 1/3, because 3 * 1/3 = 1. In ordinary arithmetic, every number except 0 has a reciprocal. In our algebraic structure above, the reciprocal of 3 is 7, because 3 * 7 = 1.
Problem C15
Which numbers have a reciprocal in this system?
Tip: You can use the multiplication table above to find reciprocals. Not all numbers have reciprocals in this system!
Take It Further: Problem C16
What’s common among all the numbers that have reciprocals? What’s common among all the numbers that don’t have reciprocals?
Tip: Think about the types of numbers which do not have reciprocals, then see if you can decide why.
Video Segment
This video segment describes how to find reciprocals using the table of multiplication in mod 10, followed by a short discussion of why some numbers do not have reciprocals. Watch this video segment after you have completed Problem C16.
You can find this segment on the session video, approximately 14 minutes and 43 seconds after the Annenberg Media logo.
Problem C17
Which of the properties found in units digit arithmetic are also true in ordinary integer arithmetic?
Problem C18
In ordinary arithmetic, if the product of two numbers is 0, one of them must be 0. Is that true here? What makes it work in ordinary arithmetic that doesn’t carry over to our new system?
Tip: Is there more than one whole number that is equivalent to 0 in this structure? How is this different from ordinary arithmetic?
Problem C19
Find, describe, and explain at least two patterns in each table that you haven’t yet used.
Tip: Is there any relationship between rows of numbers that are inverses?
Take It Further:
During the 19th century, mathematicians expanded number systems into larger sets. This led to the development of the concepts of groups and fields, which you can examine in the following optional problems.
Take It Further
The development of mathematical structures in the 19th century included the expansion of number systems into larger sets. Mathematicians studied the properties of these sets, and their operations, so that equations in any system would have roots in the new expanded system. These explorations led Galois to develop the concept of what is now known as a group. The definition of a group is as follows:
Note: Optional Problems
With a set S and an operation *, S is a group under * if all four of these are satisfied (Note that one this page, the “*” represents any binary operation, and not only multiplication as elsewhere in this Part.):
| 1. | S is closed under * |
| 2. | S is associative under * |
| 3. | S has an identity element under * |
| 4. | Every element of S has an inverse |
S can be any set of objects, and * can be any binary operation. Here is more information about each of these. (Note that in this Part, the “*” represents any binary operation, and not only multiplication as in previous Parts.)
S is closed under * if the operation always produces outputs within S. The set of whole numbers is closed under addition and multiplication — add two whole numbers, and the answer is always a whole number. The set of whole numbers is not closed under subtraction or division, however, since the output is not always a whole number.
Problem C20
Which of the following sets are closed under addition? Which are closed under multiplication? Which are closed under division?
| a. | Positive whole numbers: {1, 2, 3, 4, …} |
| b. | Full set of integers: {…, -3, -2, -1, 0, 1, 2, 3, …} |
| c. | All real numbers on the number line |
| d. | Positive real numbers |
| e. | Positive odd integers: {1, 3, 5, 7, …} |
S is associative if, for elements a, b, and c in S, (a * b) * c = a * (b * c). This property is especially useful in solving equations.
S has an identity element “e” if, for every element a in S, a * e = a and e * a = a. Then, e is the identity. Zero is the identity for addition, and 1 is the identity for multiplication.
S has inverses if, for every element a in S, there is an element b in S for which a * b = e, the identity. The inverse of 3 under addition is -3, and the inverse of 3 under multiplication is 1/3. If a set S has no identity under *, it cannot have inverses.
Problem C21
Which of these sets and operations have an identity element? Which have inverses?
| a. | Positive whole numbers, under addition |
| b. | Positive whole numbers, under multiplication |
| c. | Full set of integers, under addition |
| d. | Full set of integers, under multiplication |
| e. | Full set of integers, under division |
All mathematical groups share these four fundamental properties. Many groups are also commutative if a * b = b * a for any elements in S.
Another related concept is a mathematical field. If a set S has two operations (usually + and x) defined on it, it is a field if all of these properties hold:
| 1. | (S, +) is a commutative group |
| 2. | (S, x) is a commutative group when the identity of the first operation is removed |
| 3. | The first operation, +, is distributive over the second operation, x. This means that for any elements a, b, and c in S, it must be true that a * (b + c) = (a * b) + (a * c). |
This is a total of 11 properties. While it is rare for a set and two operations to be a field, many mathematical properties of one field translate directly to any other field.
The real numbers are a field under addition and multiplication.
Problem C22
Which of these are fields under the operations of addition and multiplication?
| a. | Positive real numbers |
| b. | Rational numbers (integers and fractions) |
| c. | Even numbers: {…, -4, -2, 0, 2, 4, …} |
| d. | Mod 4 |
| e. | Mod 5 |
Note 4
We are all familiar with our real number system. It’s one thing to be handed a system and to learn how to work in it; it’s another to see how a system evolves and then work in it. In this session, we’ll develop an algebraic system and work in it.
Suppose you’re interested in looking at units digits of whole numbers. Think about this problem:
Find the units digit of 364 * 123 + 48 * 135.
Groups: Take five minutes or so to come up with a solution. (You may have to review order of operations.) Share solutions, along with how you thought about the problem. In particular, discuss whether there is some way to do this problem without doing all the actual calculations. Have the whole group suggest possibilities. Be sure to discuss why you can just look at units digits.
Note 5
Groups: Work on Problems C1-C5.
What you have developed in Problems C1-C5 is a “units digit arithmetic,” an arithmetic whose objects are the digits 0 through 9, and whose operations are “add and take the units digit” and “multiply and take the units digit.” The whole system can be captured in the two tables provided. These tables define an algebraic structure on the set of numbers {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Note 6
Groups: Read the text before Problems C6-C19, and then work on these problems in small groups. Share what patterns you see in the table.
Note: Optional Problems
This part introduces some key mathematical terms involved in current work in algebraic structures. All groups share these properties, and all groups share certain methods for solving equations (specifically, solutions involving inverting operations). It is as important to show examples of algebraic structures which are not groups in order to understand the relationship between structures which are groups.
Groups: Work on Problems C20-C22 in small groups.
Problem C1
Don’t forget about the order of operations. The units digit will be identical to that of (4 * 6) + (3 * 4), or 4 + 2 = 6.
Problem C2
The units digit of the second number is the same as that of (2 * 2) + (6 * 2), or 4 + 2 = 6. Therefore, it’s true.
Problem C3
The units digit is the same as that of (2 * 3 + 7 * 7) * (8 + 5 * 8 * 8 * 8), or (6 + 9) * (8 + 0), or 5 * 8 = 0.
Problem C4
Yes, this is true. At each step, we reduce our calculation to the units digit — for example, 7 * 7 = 49, so we use 9. The end result is the units digit of the sum, or product, of all the units digits used throughout. We can do this only because things that occur in the tens digit, or any other higher digit, cannot affect the result in the units digit.
Problem C5
When dividing by 10, the quotient will always be the number, beginning with the tens digit. For example, 7,536 divides into 10 a total of 753 times. The remainder is, therefore, the units digit only.
Problem C6
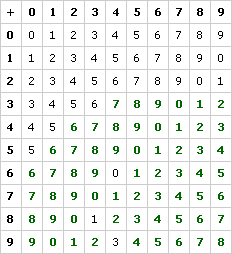
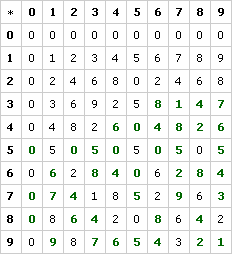
Problem C7
No, order doesn’t count. This can be seen from the symmetry in the table — each side of the main diagonal is identical.
Problem C8
Because addition on numbers is commutative already (a + b = b + a), we would expect the remainder of two identical numbers to still be identical. So our table, made of remainders, must be commutative.
Problem C9
No. Again, both sides of the main diagonal are identical.
Problem C10
Multiplication on numbers is commutative (ab = ba), so our table of remainders, based on a full multiplication table, must also be commutative.
Problem C11
Sure, adding 0 to an original number doesn’t change it, so it cannot change the remainder.
Problem C12
Yes. It can be read from the table: we want to find the second number that makes the sum 0. In each row and column of our table, 0 occurs exactly once, so there is a single opposite number for each given number.
Problem C13
If our number is n, the opposite is (10 – n). If our number is 0, the opposite is 0, since 10 is not in the system.
Problem C14
Sure, multiplying by 1 won’t change an original number, so it can’t change the remainder.
Problem C15
Only 1, 3, 7, and 9 have reciprocals, since they each have exactly one 1 in their rows and columns of the table. No other number has any 1 in its row or column.
Problem C16
The numbers 1, 3, 7, and 9 are all the numbers that do not share a common factor with 10. This allows the 1 to appear as a units digit. For example, multiples of 2 will all be even, so there cannot be a multiple of 2 that ends with a 1. The same is true of any number that shares a common factor with 10, so these do not have reciprocals. It is more difficult to guarantee (prove!) that the others must have a single 1 in their rows and columns, but a useful observation is that each number of 0 through 9 occurs exactly once in these numbers’ rows and columns.
Problem C17
For addition and multiplication, both systems have commutativity, associativity, and identity. In both systems, every number has an opposite.
Problem C18
No, it isn’t true — for example, 5 * 4 = 0. One explanation is that there is now more than one number that equals 0: 10, 20, 30, 40 … . If we can find two numbers that multiply to make any multiple of 10, this will be a 0 in our table. Also, there are numbers in our table that share factors with 10, so it is possible to find a pair that creates a multiple of 10. This is not possible in ordinary arithmetic, because no number has 0 as a factor.
There is a lot more here; you might try making the same table with other bases. Low numbers are good starting points, because their tables are easy to produce. Some tables do have the property that if two numbers multiply to 0, one must be 0 — maybe you can find which ones.
Problem C19
All are closed under addition, except for the odd integers. All five sets are closed under multiplication. The only set which is closed under division is the positive real numbers.
Problem C20
All are closed under addition, except for the odd integers. All five sets are closed under multiplication. The only set which is closed under division is the positive real numbers.
Problem C21
| • | The first set does not have identity or inverses. The identity should be 0, but 0 is not in the set. |
| • | The second set has identity, but does not have inverses. The identity, 1, is in the set, but most numbers do not have inverses. |
| • | The third set has identity and inverses. The identity, 0, is in the set, and every number has an inverse (its opposite). |
| • | The fourth set has identity, but does not have inverses. The identity, 1, is in the set, but most numbers do not have inverses. |
| • | The fifth set has neither identity nor inverses. There is no identity element for division; many people think 1 is the identity, since 7 / 1 = 7 works for any number. However, 1 / 7 = 7 would also have to be true, and it is not. |
Problem C22
| • | The first set is not a field, since there is no identity for addition (0 is not in the set). |
| • | The second is a field. |
| • | The third is not a field, since there is no identity for multiplication (1 is not in the set). |
| • | The fourth is not a field, since one element (2) does not have an inverse under multiplication. |
| • | The fifth is a field. |