Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Proportional Reasoning Homework
Session 4, Homework
Problem H1
Sandy made some iced tea from a mix, using 12 tablespoons of mix and 20 cups of water. Chris and Pat thought it tasted great, but they needed 30 cups of tea for their party. Lee arrived, and they found they disagreed about how to make 30 cups that tasted just the same:
| Chris | It’s easy: Just add 10 tablespoons of tea and 10 cups of water. Increase everything by 10. |
| Pat | Wait a minute. 30 is just 1 and a 1/2 times 20, so since you add 1/2 as much water, add 1/2 the tea: add 10 cups of water and 6 tablespoons of tea. |
| Sandy | I think about it this way: We used 12 tablespoons for 20 cups, so 12/20 = 3/5 tablespoons for 1 cup, so for 30 cups we should use 30 x 3/5 = 18 tablespoons. |
| Lee | Wait: 20 – 12 = 8, so you want to keep the difference between water and tea at 8. Since there are 30 cups of water, we should use 30 – 8 = 22 tablespoons of tea. That will keep everything the same. |
Critique each of these methods. Which methods are the same? Which methods will really produce tea that tastes the same?
Tip: Which are absolute comparisons, and which are relative ones? What type of comparison is more useful here?
Problem H2
- Draw a right triangle with legs 3 and 4 cm and hypotenuse 5 cm.
- Draw a triangle whose legs are double those in H2(a).
- Draw a triangle whose side lengths are each 2 cm more than those of the first triangle.
That is, the lengths are 5 cm, 6 cm, and 7 cm. - Which of the new triangles looks similar to the original triangle?
Problem H3
Five brothers ran a race. The twins began at the starting line. Their older brother began behind the starting line, and their two younger brothers began at different distances ahead of the starting line. Each boy ran at a fairly uniform speed. Here are the rules for the relationship between distance (d meters) from the starting line and time (t seconds) for each boy.
| Adam | d = 6t |
| Brett | d = 4t + 7 |
| Caleb | d = 5t + 4 |
| David | d = 5t |
| Eric | d = 7t – 5 |
- Which brothers are the twins? How do you know?
- Which brother is the oldest? How do you know?
- For each brother, describe how far from the starting line he began the race and how fast he ran.
Tip: Which number in each equation is related to that brother’s speed? A table may help you to see the relationship. - Which line below represents which brother? What events match the intersection points of the lines?
- What is the order of the brothers 2 seconds after the race began?
- Which two brothers stay the same distance apart throughout the race?
How do you know, based on their graphs?
How do you know, based on their equations? - If the finish line was 30 meters from the starting line, who won?
- Which brothers’ relationships between distance from the starting line and time are proportional? How do you know?
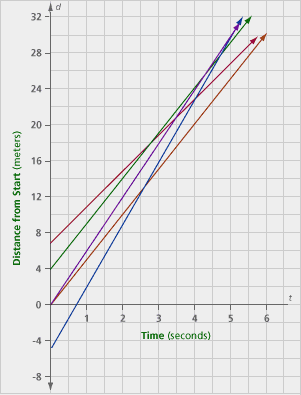
Problem H3 taken from IMPACT Mathematics Course 2, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p.331-332. www.glencoe.com/sec/math
Solutions
Problem H1
Chris’s method will produce tea that has too much mix. This method would work only if the original recipe called for the same amount of tea and water, which it doesn’t. In terms of fractions, 22/30 is not the same proportion as 12/20.
- Pat’s method is correct: 6/10 is the same proportion as 12/20, so the new mixture will have the right proportion of mix.
- Sandy’s method is also correct: 18/30 is the same proportion as 12/20.
- Lee’s method is identical to Chris’s method. If you keep the difference between tea and water the same, there will be too much tea mix added at 30 cups.
- Chris and Lee’s suggestions are incorrect because they are absolute comparisons, where a relative comparison is needed to keep the proportion of tea mix the same.
Problem H2
d. The triangle with side lengths 6, 8, and 10 is similar looking. A good comparison is the measures of the three angles of the triangle.
Problem H3
- The twins are Adam and David. We know they start at the starting line, so they must be the ones without any constants in their equations.
- The oldest must be Eric, since he is the one whose equation includes the instruction “-5”, which means he begins 5 meters behind the starting line.
- Adam started at the starting line, and ran at 6 meters per second. Brett started 7 meters ahead, and ran at 4 meters per second.
Caleb started 4 meters ahead, and ran at 5 meters per second.
David started at the starting line, and ran at 5 meters per second.
Eric started 5 meters behind the starting line, and ran at 7 meters per second.
- The points of intersection on the graph represent when one brother passes another during the race. Their times (on the horizontal axis) and their distance from the start (on the vertical axis) are the same.
- Use t = 2 in all five equations, or refer to the graph. The order is: Brett (15 m), Caleb (14), Adam (12), David (10), and Eric (9).
- Caleb and David, who run at the same speed. We know this because their graphs form parallel lines, which always stay the same distance apart.
- Find the finishing times for the five by solving the equations for d = 30, or referring to the graph (draw a horizontal line at distance d = 30). Solving the equations shows that Adam and Eric tie for first (5 seconds), then Caleb (5.2), Brett (5.75), and David (6 seconds).
- Adam and David. Their graphs pass through the origin (0, 0) and their equations are in the form y = kx.
