Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
The scientists at the research lab for Whodunit Jeans are trying to decide on just the right shade of blue for a new line of jeans. Being scientists, not mathematicians, the researchers decide to choose a color by mixing pure blue liquid and clear water together until they get just the right shade. Note 3
The scientists have several beakers of liquid, some with blue liquid and some with clear water. They plan to mix these together in big bowls. Before they mix the liquids, they guess how blue the mixture will be.
In Problems B1-B7, there are two sets (A and B) of blue-clear combinations to mix. Predict which set will be bluer, and explain your reasoning. Assume you do not know how to compare fractions with unlike denominators. (Converting to a common denominator and comparing would make these problems trivial.) Note 4
Problem B1
![]()
Tip: Consider whether you are making absolute or relative comparisons in Problems B1-B7.
Problem B2
![]()
Problem B3
![]()
Problem B4
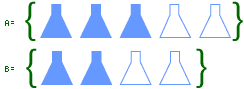
Problem B5

Problem B6

Problem B7

| Video Segment
In this video segment, Frederick uses relative comparison to solve Problem B4. Watch this segment after you have completed Problems B1 through B7 and compare your reasoning with Frederick’s. Why would an absolute comparison not be useful in solving Problems B1-B7? You can find this segment on the session video, approximately 18 minutes and 48 seconds after the Annenberg Media logo. |
Some of the scientists in the lab decided to see what would happen if they took two different mixtures and mixed them together. They called this the “union” of the two mixtures. For example, in Problem B4, they took the two mixtures A and B and formed the union of the mixtures. Standard mathematical notation for the union of two things (usually sets) is U, so they named their new mixture A U B.
Problem B8
In this example, which is bluer: A, B, or A U B?

Problem B9
What can you say about the relative “blueness” of A and B if A U B is bluer than A? If it is bluer than B?
Tip: Your results from Problems B1-B7 may be helpful here.
Problem B10
Can A U B ever be bluer than both A and B? If not, why? If so, when? Note 5
Tip: Consider this problem from a practical standpoint.
Problem B11
Can A U B ever be just as blue as either A or B? If not, why? If so, when?
Someone invented a term called the “blueness quotient” (BQ) of a mixture. In the mixture in Problem B4, the BQ of A is 3/5, and the BQ of B is 2/4.

Problem B12
Come up with a rule for computing the BQ of A U B if you know the BQs of A and B.
Problem B13
Mixture A has a BQ of 1/3, and the lab has decided that it would like A U B to have a BQ of 1/2. What could be the BQ of mixture B? Is there more than one answer? Why?
Note 3
We will now look at ways to compare ratios in the context of mixing colors. In these problems, it is important to understand that we’ll be thinking about these mixtures without using the common algorithms for comparing fractions. That is, we need to assume we don’t have the skills for finding a common denominator to compare — for example, 4/7 and 3/8. This forces us to compare ratios by relying on a more basic understanding of what a ratio is.
Note 4
Groups: Work in pairs on Problems B1-B13. Discuss solutions to Problem B5 in particular.
Consider the following solution:
In mixture A, there is one more blue beaker than clear, and in mixture B, there is one more blue beaker than clear. Therefore, the mixtures are the same color.
Try to find the fault in this explanation. This is the same reasoning, by the way, that students use when they claim that 2/3 is the same as 3/4, since the numerator in each fraction is one less than the denominator. They are, in fact, using additive strategies.
A lovely way of solving mixture problems like this is by comparing the effect these containers have on the entire mixture. For example, if mixture A had 2 clear containers and 3 blue, and mixture B had 99 clear containers and 100 blue, the extra blue in A would have a greater effect on the entire mixture than the extra blue in B which is spread over 199 total containers. Therefore, A would be bluer (3/5 compared to 100/199).
Some people may use a canceling technique to compare these ratios. They will form blue/clear container pairs and cross them out. For example, in Problem B6, they will cancel all the containers in A after forming 2 blue-clear pairs, and do the same in B with 1 clear left over, claiming that B is less blue. This technique will not work in Problem B5, however, since after using the “canceling” technique, each mixture has 1 blue container left, suggesting they’re the same shade of blue. Once again, though, the effect of the extra blue in A is greater than the effect in B because there are fewer containers in A.
Another approach to these problems is to equalize the number of containers in each situation by creating multiples of mixtures. For example, in Problem B7, if you double mixture B, you get the same number of containers as in mixture A, making them easy to compare.
Note 5
Problem B10 is an interesting one and may require spending some time thinking about how to prove this assertion. In fact, A U B can never be bluer than both A and B. You can use some algebra to prove this. Find a relationship between a, b, c, and d such that: (a + c) / (b + d) is greater than a/b and (a + c) / (b + d) is greater than c/d. These two inequalities become: c / d is greater than a / c and a / b is greater than c / d, a contradiction. Therefore, A U B can never be bluer than both A and B.
Problem B1
A will be bluer, because B’s mix is the same as A’s, but with two additional clear beakers thrown in.
Problem B2
B will be bluer. Its mix is the same as A’s, but with an extra blue beaker thrown in.
Problem B3
B will be bluer, for the same reason as in Problem B2. Or, consider what would happen if you tried to make equal doses of A and B. (Common denominators!)
Problem B4
A will be bluer. One explanation is that B is half blue, while A is more than half blue.
Problem B5
A will be bluer. A and B each have one more blue than clear beaker, but in A, each beaker makes more of a difference. In other words, A has 1/5 more blue than clear, and B has 1/7 more blue than clear, and since 1/5 is larger than 1/7, A is more blue. Another explanation is that to get B from A, you would need to add 1 blue and 1 clear beaker, which (as a mix) is lighter than A. Therefore, B will end up being lighter than A.
Problem B6
A will be bluer. Its mix is the same as B’s, but with one less beaker of clear water.
Problem B7
They are identical in color. One explanation is that each mix has twice as much blue as clear. A second explanation is that mixture A can be made by doubling the ingredients of mixture B.
Problem B8
The bluest is A. A is already bluer than B, so adding B’s mix into A won’t make it a deeper blue (think of what would happen with paint). This means that A U B cannot be bluer than A, so A is the bluest of the three. Another explanation is that A has one more blue than clear, and so does A U B, but in A U B the extra blue does not contribute as much to the mixture (since there are more beakers of liquid in it).
Problem B9
If A U B is bluer than A, then B must be bluer than A. This is true because A U B is formed by adding B to A; if we add something to A and it becomes a deeper blue, whatever we added (B) must be bluer than what we started with (A). The reverse is also true: If A U B is bluer than B, then A is bluer than B.
Problem B10
No such magical mixing device exists. Take the bluer of A and B; A U B can never be bluer than it. You could also solve this problem using algebra and common denominators.
Problem B11
Yes, but only if A and B are equally blue. If A is bluer than B, adding B dilutes A, and the result (A U B) will not be as blue as A. If A and B are equally blue, A U B will be identical to both.
Problem B12
Use the total number of blue beakers, divided by the total number of beakers used. If the BQ of A is M / N and the BQ of B is P / Q, then the BQ of A U B is (M + P) / (N + Q).
Problem B13
There are several possible BQs for mixture B. Mixture B could contain only one beaker of blue (BQ = 1/1). A U B would then have BQ 2/4 = 1/2. If we wanted A U B to have BQ 3/6 (an equivalent fraction to 1/2), then mixture B would have to have BQ 2/3. Mixture B can have BQ 1/1, 2/3, 3/5, 4/7, 5/9, or any fraction of the form N / (2N – 1). Mixture B’s only requirement is that it must have a BQ larger than 1/2 (see Problem B10 for the reasoning).