Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Classroom Case Studies, Grades 3-5 Part D: More Problems That Illustrate Algebraic Thinking (25 minutes)
Session 10: 3-5, Part D
At the 3-5 grade level, there are many problems that prepare students for their later work in algebra. Experiences with these problems can also build bridges between arithmetic and algebra, while increasing the students’ chances for success in future mathematics. Note 7
In this section we’ll analyze problems at the 3-5 level for their algebraic content. For each problem, find a mathematical solution, then answer questions (a)-(f) listed below.
| a. | What algebraic content is in the problems? |
| b. | What content does it prepare students for later? |
| c. | How does this content relate to the mathematical ideas in this course? |
| d. | How would your students approach this problem? |
| e. | What are other questions that might extend students’ thinking about the problem? |
| f. | Does your current program in mathematics at your school include problems of this type? |
Problems
Problem D1
There are red (R) and black (B) marbles in a box in the drawer. Take out some marbles so that there are 3 red marbles for each black marble left in the box.
a. What is the fewest marbles you must take from the box?
b. Draw a picture of the marbles left. Mark B or R to show the color of each marble.
c. Tell how you decided how many to take out.
Problem D2
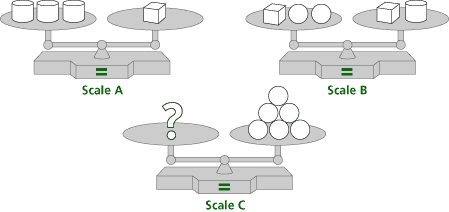
| a. | Which block, cube, cylinder, or sphere will balance Scale C? |
| b. | List or draw the steps you followed to identify the block. |
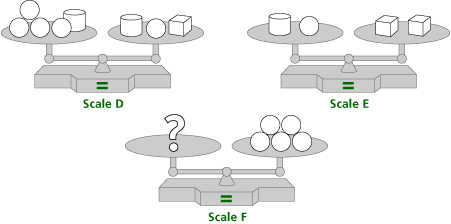
| c. | Which block, cube, cylinder, or sphere will balance Scale F? |
| d. | List or draw the steps you followed to identify the block. |
Problem D3
a. Find the weight of each block.
cylinder = ________ pounds
sphere = ________ pounds
cube = ________ pounds
b. List or draw the steps you followed to find the weights of the blocks.
c. Find the weight of each block.
cylinder = ________ pounds
sphere = ________ pounds
cube = ________ pounds
d. List or draw the steps you followed to find the weights of the blocks.
Problem D4
For each Start number, give the End number.
For example, when the start number is 5, here’s how you get to 21, the End number.
(Start) 5 + 2 = 7; 7 x 3 = 21 (End)
| a. | Start: 0; End: ________ |
| b. | Start: 1; End: ________ |
| c. | Start: 3; End: ________ |
When the End number is 24, the Start number is 6.
For each End number, give the Start number.
For example, when the End number is 24, here’s how you get to 6, the Start number.
(End) 24 / 3 = 8; 8 – 2 = 6 (Start)
| d. | End: 12; Start: ________ |
| e. | End: 21; Start: ________ |
| f. | End: 36; Start: ________ |
Problem D5
In the following table, the same shapes are the same numbers. The numbers in the circles are sums, reached by adding across and adding down.
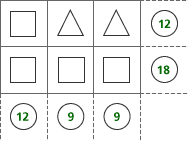
| a. | What number is the square? |
| b. | What number is the triangle? |
| c. | Explain how you found the numbers. |
Problems adapted from Groundworks: Algebraic Thinking, Grade 5, by Carole Greenes and Carol Findell (New York: Creative Publications, Wright Group/McGraw-Hill 1998).
The above material may not be reproduced without the written permission of Wright Group/McGraw-Hill.
Notes
Note 7
It is often difficult for teachers to see how the mathematics content at their grade level builds algebraic thinking. In this part, we’ll look at many examples of elementary mathematics that build bridges to algebraic thinking.
Groups: Work on the problems from Groundworks, recording answers to questions (a)-(f) as you do each problem. It is important to identify the mathematical content in each of the problems and how that content illustrates algebraic thinking.
Solutions
Problem D1
The answers are: Take out four black marbles; the picture should include six red and two black marbles. The mathematical content is proportional reasoning.
Possible responses to the questions to consider:
| a. | This prepares students for reasoning with proportions, recognizing equivalent ratios, and using drawings to help solve problems. | ||||||||
| b. | This content requires the uses of proportional reasoning, and all the skills related to patterns: finding, describing, explaining, and using patterns to predict. | ||||||||
| c. | This problem makes use of proportional reasoning discussed in Session 4 and all the skills related to patterns discussed in Session 2 (finding, describing, explaining, and using patterns to predict). | ||||||||
| d. | Students approach these problems in several ways:
|
||||||||
| e. | To extend students’ understanding, ask questions such as the following:
|
||||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D2
For the first set of scales the answer is 1 cube
For the second set of scales the answer is 1 cylinder.
Possible responses to the questions to consider:
| a. | The mathematical content is balance, the notion that the objects on the lower pan on a pan balance weigh more than the objects on the higher pan, and that one object that balances with two or more objects is the heaviest. This prepares students for understanding equality as balance and the notion that adding or removing the same items from both sides of a balance retains balance. | ||||||||
| b. | This content introduces equality as balance to set the stage for solving equations by manipulating equations while maintaining balance. | ||||||||
| c. | This content illustrates methods for solving linear equations. | ||||||||
| d. | Students approach these problems in several ways. One way is shown for each problem.
|
||||||||
| e. | To extend students’ understanding, ask students to describe other ways to solve the problems or to make up weights for each block that would preserve the balance, and ask questions such as the following:
|
||||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D3
The answer for the first set of scales is: cylinder = 4, sphere = 3, cube = 5
The answer for the second set of scales is: cylinder = 6, sphere = 4,
cube = 2
Possible responses to the questions to consider:
| a. | The mathematical content is variable and solving three equations in three variables. | ||||||||
| b. | This content prepares students for understanding that they can replace a variable with its value. | ||||||||
| c. | This content illustrates methods for solving systems of linear equations. | ||||||||
| d. | Students approach these problems in several ways. One way is shown for each problem.
|
||||||||
| e. | To extend students’ understanding ask questions such as the following:
|
||||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D4
Answers: 6, 9, 15, 2, 5, 10
Possible responses to the questions to consider:
| a. | The mathematical content is function. | ||||||||||||
| b. | This content prepares students for understanding function as a sequence of computations. | ||||||||||||
| c. | This content illustrates the use of inverse operations. | ||||||||||||
| d. | Students approach these problems in several ways. One way is shown here.
|
||||||||||||
| e. | To extend students’ understanding, ask questions such as the following:
|
||||||||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D5
Answers: The square is 6 and the, triangle is 3.
Possible responses to the questions to consider:
| a. | The mathematical content is variable. | ||||||
| b. | This content prepares students for solving two equations with two variables. | ||||||
| c. | This content illustrates the use of division and replacement to solve equations. | ||||||
| d. | Students approach these problems in several ways. One way is shown here. Column 1 shows the sum of two squares is 12. That means that one square is 6 (12 ÷ 2). Column 2 shows the sum of one triangle and one square is nine. Replace the square with six. That means that the triangle is 3 (9 – 6). |
||||||
| e. | To extend students understanding, ask questions such as the following:
|
||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
