Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
We have been using the equal sign throughout previous sessions. In this part we are going to look at the meaning of equality, which will give us some insight on using equality and its properties to solve equations.
Note 2
Examine the following equations. Each equation makes a statement about quantities. Is each statement true always, sometimes, or never? Think about your reasoning for each statement.
If someone asked you to solve the equations in Problem A1, what would the solution sets be?
Tip: The definition of a solution set is helpful here. Consider how many different solutions there are in each solution set.
|
Video Segment In this video segment, Gina explains her solution to Problem A2, including how she generated a rule for the number of toothpicks in each row of squares. Watch the segment after you have completed Problem A2. If you get stuck on the problem, the video segment may help you come up with a solution. Does Gina’s work involve a closed-form description or a recursive description for the number of toothpicks in each new row? Refer to Session 2, Part E for more information on these two kinds of descriptions. You can find this segment on the session video, approximately 3 minutes and 9 seconds after the Annenberg Media logo. |
A chalkboard reads: 10 + 21 = ?
A balance scale is a good visual model for representing an equivalence relationship. Picture a two-pan balance scale, with two weights on the left side and one on the right. If the weights on the left side are 10 and 21 grams, and the weight on the right side is 31 grams, the scale will be balanced. Note 3
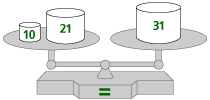
As you will see in Part C, using balance scales is also a good transition to more formal, symbolic techniques for solving equations.
Problem A4
In this balance puzzle, determine what will balance with the rectangle in the third scale. Throughout the three scales, the same shape always has the same weight.
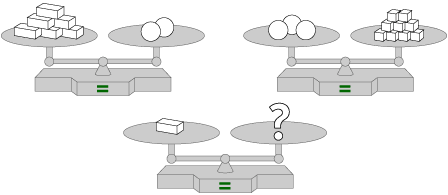
Video Segment
In this video segment, Frederick explains his solution to Problem A4. Watch the segment after you have completed Problem A4 and compare your strategy with Frederick’s. If you get stuck on the problem, you can watch the video segment to help you.What strategies did you use to solve the problem?
See if you can use Frederick’s or your own strategy to solve the following problems.You can find this segment on the session video, approximately 5 minutes and 51 seconds after the Annenberg Media logo.
Problem A5
What might be a solution for scale D, assuming that the same shapes have the same weight?
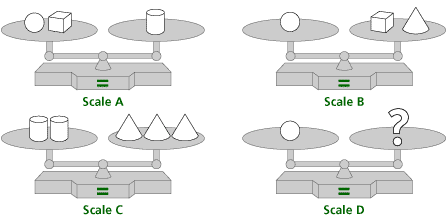
Tip: Think about the strategies used by Frederick in this video segment. Additionally, think about what you can do to each side of a scale while keeping it balanced. Any such step can be done to any of the scales above.
Problem A6
What might be a solution for scale D, assuming that the same shapes have the same weight? Note: The shapes in this problem may not be the same weight as the shapes in the previous problem.
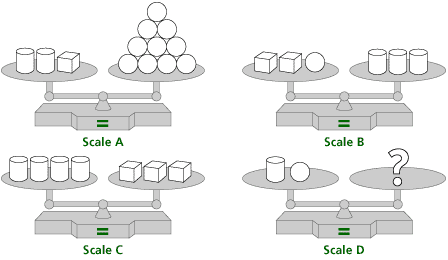
Tip: Think about the strategies used by Frederick in this video segment. Additionally, think about what you can do to each side of a scale while keeping it balanced. Any such step can be done to any of the scales above.
Problem A7
Look at the following equations from Problem A1. For each equation, draw a balance scale to represent the equation. How can you use balance to decide when an equation is true or false?
Note 2
The problems in this section use the balance scale as a model for the equality relationship.
Groups: Discuss Problems A1-A3 as a whole group before going on to solve the balance scale puzzles.
For the equation in Problem A3, the equal sign acts as a symbol for students to do something or to perform the given operation. In other words, the equal sign connotes “give the answer to what comes before.” This is a beginning notion of equality that at times interferes with a broader concept of equivalence. In fact, many students in elementary and middle school will argue that the equation in Problem A1(c) is impossible because “y” is not an “answer.”
Although the equal sign signifies an equivalence relationship in all of the equations, the solution sets are different for some of the equations.
Note 3
Groups: After discussing Problems A1-A3, work in pairs or small groups on the balance problems in Problems A4-A6.
Look for ways to think about replacing specific shapes for other shapes. The point here is not to use algebraic notation or equations to represent these situations. This sort of reasoning is essential in making the transition to solving equations, so it’s an important step in the process.
Groups: Share solutions with the whole group, making sure to attend to the kind of reasoning used in solving the problems.
Problem A1
Problem A2
Problem A3
Problem A4
The solution is that 1 rectangle will balance with 1 square. While it would also be correct to say that 1 rectangle will balance with 1/3 of a circle, this answer does not reflect use of the second scale.
Problem A5
One possible answer is that, for scale D, the circle is equivalent to 5 cubes. The cone is equivalent to 4 cubes, and the cylinder is equivalent to 6 cubes.
Problem A6
One possible answer is that, for scale D, the cylinder and circle are equivalent to 1 cube. The cylinder is equivalent in weight to 3 circles, and the cube is equivalent to 4 circles.
Problem A7
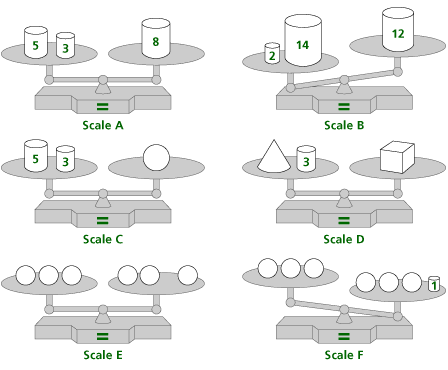
Each scale is balanced only if the quantities on each side of the scale are equivalent. In the same way, an equation is true only if the quantities on each side of the equal sign are equivalent. When variables are used, the scale may be balanced always (as it is in equation (e)), sometimes (as in equations (c) and (d)), or never (as in equation (f)).