Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
You know that for linear functions, the difference between successive outputs is a constant. For exponential functions, the ratio between successive outputs is a constant. Is there some similar pattern for quadratic functions? The next few problems will help you decide. Note 12
As described at the end of Part C, quadratic functions involve squaring an input. The simplest quadratic function is simply output = (input)2. Here’s the start of a table for this function, with three columns: input, output, and the difference between successive outputs:
| n | n2 | Difference between outputs | ||
| 0 | 0 | |||
| 1 | 1 | 1 | ||
| 2 | 3 | |||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 |
Fill in both the missing outputs and missing differences. Describe a pattern in the differences. Are the differences constant? Note 13
Tip: Remember, “constant” means the number remains the same: 5, 5, 5, … . A pattern may or may not be a constant pattern.
Problem D2
Add a new column to your table like the one shown below. In this column, put the “differences between differences,” called the second differences. What do you notice?
| n | n2 | Difference between outputs | Second differences | ||
| 0 | 0 | ||||
| 1 | 1 | 1 | |||
| 2 | 3 | 2 | |||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
|
Video Segment This video segment shows how to create a table of first differences and second differences in the equation y = x2. Watch this segment after you’ve completed Problem D2. If you get stuck on the problem, you can watch the video segment to help you. You can find this segment on the session video, approximately 15 minutes and 42 seconds after the Annenberg Media logo. |
Problem D3
In Part C, you built a table for triangular numbers. One way to write the rule for triangular numbers is
output = (n2 + n) / 2.
Create a table for this rule for triangular numbers, and look for patterns in the first and second differences.
| n | (n2 + n) 2 |
Difference between outputs | Second differences | ||
| 0 | 0 | ||||
| 1 | 1 | 1 | |||
| 2 | 3 | 2 | |||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
A quadratic function is any function that can be written as…
output = A(input)2 + B(input) + C
A, B, and C can be any number. The only exception is that A cannot equal zero — if A were zero, there would be no need for the input to be squared!
Problem D4
Create your own quadratic function. Tabulate it and look at the differences and second differences. What seems to be true about quadratic functions?
In this session, we’ve seen some of the differences between linear functions, quadratic functions, and exponential functions and learned about their practical uses. The following Interactive Activity presents a graphical comparison between three functions that have similar equations but very different graphs:
y = 2x
y = x2
y = 2x
Problem D5
Which of these is an exponential function? Which is a quadratic function? Which is a linear function? For each, explain how you know.
Note 12
In this last part of the session, we’ll look at differences between successive outputs of quadratic functions. Successive outputs do not produce constant differences (as with linear functions) or constant ratios (as with exponential functions), but the differences do have a pattern nonetheless. It turns out that for quadratic functions the differences are linear, and the second differences — the differences of differences — are constant.
Note 13
Groups: Work on Problems D1-D4 with a partner. Share results and describe the functions created for Problem D4. Out of this work, a conjecture should emerge that the second differences of quadratic functions are constant.
If there’s time, finish the session by looking for what the second difference tells you about the function. For a linear function, the difference between outputs is the same as the coefficient of x in the linear equation, and the same as the slope of the line.
Look at several different quadratic functions and the corresponding second differences. Notice that half of the second difference is the coefficient of the x2 term in the equation.
Looking back at the figurate numbers, for example, the square numbers had a formula y = x2. The coefficient of x2 is 1, and the second differences were constant 2s. The triangular numbers had a formula y = x2/2 + x/2. The coefficient of x2 is 1/2, and the second differences were constant 1s.
Look for the constant second differences for the pentagonal and hexagonal numbers, and use those to help find the more difficult formulas for these numbers.
Groups: Sharing results will allow you to collect information about quadratic functions. End the session by adding quadratic and exponential functions to the list of nonlinear functions started at the beginning of the session.
Problem D1
Here is the completed table:
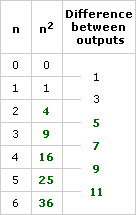
The differences are not constant, but they increase by 2 for each successive difference.
Problem D2
Here is the completed table:
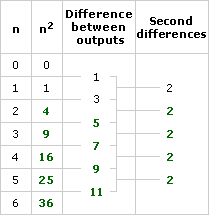
The difference between outputs forms a linear function, and the second differences are constant (in this case, they’re always equal to 2).
Problem D3
Here is the completed table:
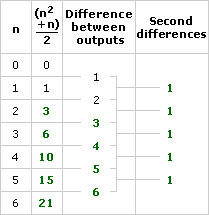
As before, the first differences form a linear function, and the second differences will always be constant.
Problem D4
You should find that with any quadratic function, the first differences will always form a linear function, and the second differences will always be constant.