Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Here are 3 balanced scales. Use your intuition about balance to determine, for each case, how many blocks have to be in the bag.
What would happen if you removed a block from the left? What would happen if you added a block to the left?
For the purposes of the problems, the bags in each problem hold the same number of blocks, and the bags themselves weigh practically nothing.
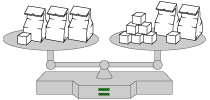 |
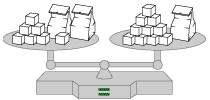 |
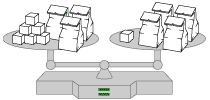 |
|
| Video Segment
In this video segment, Sue-Anne tells Professor Cossey how she solved a balance puzzle while Professor Cossey follows along on a chart. Was Sue-Anne’s thinking similar to or different from, your own strategy for these problems? Watch the video segment after you have completed the Bags and Blocks interactive activity and compare your strategy with Sue-Anne’s. If you get stuck during the activity, you can watch the video segment to help you. You can find this segment on the session video, approximately 13 minutes and 31 seconds after the Annenberg Media logo. |
You probably noticed in the Interactive Activity that in order to keep balance, you must do the same thing to both sides of the scale. In an algebraic equation, the balance is represented by the equal sign, and only doing the same thing to both sides of the equation will preserve the balance.
Note 6
Problem C1
Make up your own bag and block balance puzzle. If you are working with someone else, exchange puzzles with your partner and solve your partner’s puzzle.
Problem C2
Look at the balance puzzle below.
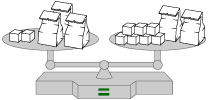
Tip: If you are having trouble here, watch the video segment following the Interactive Activity.
Problem C3
Create a balance puzzle where the solution is not a whole number of blocks. How could you modify your model to fit this solution?
Note 7
Problem C4
Draw a balance puzzle that represents 2h + 3 = h + 8. Now solve the balance puzzle. In the puzzle, what is represented by the “h” in the equation?
Problem C5
Draw a balance puzzle that represents 3b + 7 = 3b + 2. Now solve the equation. Explain what happens. Which equation below from Problem A1 is most like this one?
Note 8
Problem C6
Draw a balance puzzle that represents 4b + 3 = 4b + 3. How is this different from what happened in Problem C5? Which equation below from Problem A1 is most like this one?
Problem C7
Can you draw a balance puzzle to represent the equation 4b – 2 = 5b – 3? Why or why not? Note 9
Problem C7 brings out some of the limitations of the balance model. The method of doing the same thing to both sides may still be used to solve problems that are difficult to represent with balance puzzles.
Problem C8
Solve the equation in Problem C7 by doing the same thing to both sides.
Problem C9
One method of teaching how to solve equations is that “if you don’t like which side a number is on, move it to the other side and switch the sign.” How is this related to the method of doing the same thing to both sides?
|
Video Segment In this video segment, Sue-Anne says that the balance puzzle helped her see why it was so important to do the same thing to both sides, and emphasized the importance of using this analogy with her students. Think about the problems you’ve worked on in this session. Will the method of doing the same thing to both sides solve every problem in this session, or just some of them? |
There are many strategies that people use to solve equations: guessing and checking, backtracking or inverting operations, and doing the same thing to both sides. For any particular problem, one method may be easier than another. The word “easier,” however, has two different meanings. It might mean “more conceptually understandable,” or it might mean “more efficient to compute.” The guess-and-check method is rarely efficient, but students understand it. Backtracking or inverting operations doesn’t always work. Doing the same thing to both sides always works, but sometimes the computation is messy.
Problems in Part C taken from IMPACT Mathematics Course 2, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p. 389. www.glencoe.com/sec/math
Note 6
Now lets look at a new model for solving equations, one that works in situations where backtracking doesn’t. The model of bags and blocks focuses on the idea of balance. Each bag holds an unknown number of blocks (eventually represented by a variable). Each bag in the same problem must hold the same number of blocks, just as a variable in an equation must stand for the same number every time it is used.
The challenge is to solve a series of problems by figuring out how many blocks are in each bag. Encourage participants to solve the problems by removing the same thing from each side of the scale, which is comparable to the more formal process of doing the same thing to both sides of an equation.
Groups: Work in pairs on Problems C1-C7.
Note 7
Problem C3 brings up the interesting question of what happens when the solution is not a whole number.
Groups: Some might say that it’s possible to change the model so that the blocks are made out of some material, like clay, that can be cut up into fractions of blocks. Others might say that the model cannot be used. There is no need for consensus on this issue — the point is that when models fail, they can either be modified or abandoned for new methods.
Note 8
Problem C5 revisits an idea from the previous session: equations that have no solution. We have seen this idea modeled as two parallel lines: no intersection means no solution. This is another way to think about the same situation. Taking an equal number of bags off each side leaves unequal numbers of individual blocks, which would not balance each other. Thus the original equation was never really in balance to begin with.
Note 9
The representation of negative blocks in Problem C7 is even more difficult and is, in fact, a good example of when a model becomes more trouble than it’s worth. Many models outgrow their usefulness in this way.
Problem C2
Problem C3
One such problem has 3 bags and 2 blocks on the left, and 1 bag and 7 blocks on the right. Solving yields that each bag should have 2 1/2 blocks. One way to modify the model is to have the solution represent the relative weight of the bag rather than the number of blocks inside it.
Problem C4
The solution is h = 5. In the balance puzzle, this means that there would be 5 blocks in each bag, since h was the variable assigned to the unknown quantity.
Problem C5
There is no solution! One explanation is that no matter what value b represents, the left side of the equation will be larger than the right. Looking at the balance puzzle, there are always 5 more blocks on the left side than on the right. This is most similar to equation (f) of Problem A1, which had no solution.
Problem C6
Every number is a solution! No matter what value b represents, the left side and right side are equal. In the balance puzzle, no matter how many blocks are in each bag, the balance is maintained. Note that this means there is not enough information to find the value of b. This is most similar to equation (e) of Problem A1, which had an infinite number of solutions.
Problem C7
It can be done, but it requires some changes. One way is to represent “subtracting 2” by adding 2 blocks to the opposite side. A better way is to use items that would reduce the weight of a side, such as “negative blocks” or helium balloons. Each balloon cancels the weight of a block, so adding a block to a side would be identical to removing a balloon, and vice versa. Note that in this problem, “x” represents the number of blocks in each bag.
Problem C8
Add 3 to each side to yield 4x + 1 = 5x. Then, subtract 4x from each side to yield
1 = x, the solution.
Problem C9
Consider an equation like 3x + 5 = 23. Solving this by moving 5 to the right and switching the sign gives 3x = 23 + (-5), or 3x = 18. Solving by doing the same thing to both sides would require us to subtract 5 from both sides:
3x + 5 = 23
– 5 – 5
3x = 18
Note that this is identical in result to the solution by moving, but it also explains the origin of the -5.