Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Nonlinear Functions Homework
Session 7, Homework
You’ve already seen examples of exponential growth. When you have an exponential function where the constant multiple between outputs is less than 1, you have a decreasing function. Instead of exponential growth, you have exponential decay. Here’s an example:
The brightness of a light can be described with a unit called a lumen. A certain type of mirror reflects 3/5 of the light that hits it. Suppose a light of 2,000 lumens is shined on a series of several mirrors.
Problem H1
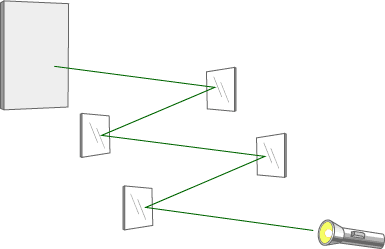
Complete the table to indicate how much light would be reflected by each of the first three mirrors. (Mirror 0 represents the original light.)
Problem H2
One mirror in the series reflects about 12 lumens of light. What mirror number is it? How did you find your answer?
Problem H3
Which mirror number reflects about 1/10 the original amount of light? Does it depend on the starting amount of light?
Problem H4
The graph below shows the amount of light reflected by another series of mirrors. The amount of light reflected by this type of mirror is different from the amount reflected by the other mirrors you investigated. The intensity of the light being shone on the first mirror is also different.
- What is the intensity of the light being shone on the first mirror?
- How much light was reflected by the first mirror?
- What fraction of light does the first mirror reflect?
- Do the other mirrors reflect the same fraction of light? That is, does this graph show exponential decay?
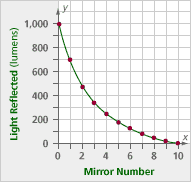
Problem H5
Suppose you have the function y = (1/5)x.
- As the value of the inputs increases, what happens to the outputs?
- Is this an exponential growth function, or an exponential decay function?
- Will you ever get 0 as an output? Explain your answer.
- Will you ever get negative numbers as outputs? Explain your answer.
- How does your answer to (c) relate to Problems H1-H4?
Homework problems taken from IMPACT Mathematics Course 3, developed by Education Development Center, Inc. (New York: Glencoe/McGraw-Hill, 2000), p.175-176. www.glencoe.com/sec/math
Solutions
Problem H1
Here is the completed table. One formula is L = 2,000(0.6)m.
|
Problem H2
The best way to do this, without using more advanced math such as logarithms, is to continue following the table. This is particularly easy with a spreadsheet. The 10th mirror will reflect about 12 lumens.
Problem H3
We’d be looking for the mirror that reflects closest to 200 lumens, which is the 5th mirror (156 lumens). The 4th mirror reflects 259 lumens; this does not depend on the starting amount of light. This means that the 6th mirror reflects about one-tenth the light of the first mirror, the 7th mirror reflects one-tenth the light of the 2nd mirror, and so on.
Problem H4
- The initial intensity is 1,000 lumens.
- The 1st mirror reflects 700 lumens.
- This fraction is 700 / 1000 = 7/10, or 70 percent.
- Yes, the 2nd mirror appears to reflect about 7/10 of 700 lumens, which is 490 lumens. The 3rd mirror reflects 7/10 of 490 lumens, which is 343 lumens. This pattern appears to continue indefinitely at a constant ratio, so it is an exponential decay situation.
Problem H5
- The outputs keep getting smaller, but remain positive, because at each stage a positive number is divided by 5.
- This is an exponential decay function, because successive outputs are getting smaller, and the base is between 0 and 1.
- Zero will never be an output, even though the outputs will become increasingly close to zero. This happens because the numerator remains 1, no matter what the value of x is, while the denominator becomes increasingly larger as x increases.
- Because two positive numbers are used in the division, a negative number can never result.
- In Problems H1-H4, this implies that even after 100 or more mirrors, some light will still be reflected, although the amount of light reflected will become increasingly small.
