Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In This Part:
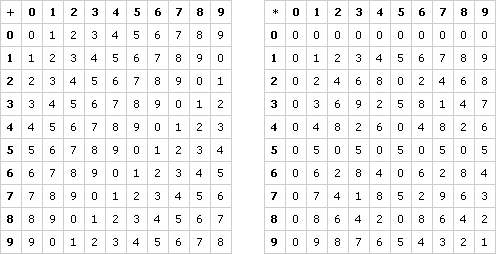
How might you solve equations in this new system? Note 7
Let’s start with the equation 3x = 8. Looking at the multiplication table, we can see that 3 * 6 = 8, so x = 6 is a solution. In fact, it’s the only solution, because there is only one “8” in the third row of the multiplication table.
Or you could reason like this: “To solve 3x = 8 in our regular system, I would divide both sides by 3. That’s the same as multiplying by the reciprocal of 3. In this system, 3 * 7 = 1, so 7 is the reciprocal of 3.”
So you can calculate as follows:
3x = 8
7(3x) = 7 * 8
(7 * 3)x = 6 (Note that in the table, 7 * 8 = 6)
x = 6
Multiplying by 7 is the equivalent of dividing by 3 in this system. If you need to subtract, you can add the opposite of a number.
If you needed to solve the equation x + 4 = 2, you could reason like this: “To solve x + 4 = 2, I want to subtract 4 from both sides. In this system, 6 is the opposite of 4, so I can add 6 to both sides in order to remove the 4.”
You would calculate as follows:
x + 4 = 2
x + (4 + 6) = 2 + 6
x + 0 = 8
x = 8
Try to solve these equations. If you have trouble, you can always use the operations table.
Problem D1
Solve the equation 7x + 5 = 9 in this system. Explain how you did it. Note 8
Tip: Remove the 5 first by adding its opposite, which is 5. Then “divide” by 7 by multiplying by the reciprocal of 7, which is 3.
Problem D2
Solve the equation 3x + 7 = 4 in this system. Explain how you did it.
Tip: Add the opposite of 7, then multiply by the reciprocal of 3.
Problem D3
Solve the equation 4x + 1 = 9 in this system. Explain how you did it.
Tip: This problem is much harder! Why? Because 4 does not have a reciprocal. There may be no solution, or there may even be more than one solution!
Problem D4
Solve the equation 4x + 1 = 8 in this system. Explain how you did it.
Take It Further: Problem D5
Describe conditions that make the equation Ax = B in this system have no solution, exactly one solution, or more than one solution. How is this different from solving equations in the real number system?
This system of “units digit arithmetic” may seem like abstract nonsense — when would you need to compute just with units digits? In fact, different algebraic systems arise in all kinds of applications. Note 9
In the past few activities, you have been looking at a modular system. The “mod 10” system means you divide by 10 and take the remainder — in other words, take the units digit. We’ll now focus on an application involving another modular system: enciphering and deciphering messages.
First, notice that you can assign each letter of our alphabet a number from 0-25:
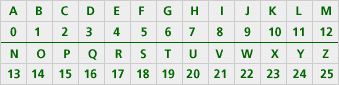
One of the oldest known substitution ciphers (a code where one letter stands for another) is the one reportedly used by Julius Caesar himself:
To get the ciphered letter, add 3 to the original letter, or “plaintext.” In symbols, this is: C = P + 3. Note 10
Problem D6
Encipher your name using Caesar’s cipher.
Problem D7
Shelly didn’t know how to encipher the “y” in her name? What should she do?
Problem D7 suggests that the algebraic description C = P + 3 is not quite right. We need some way to describe “wrapping around” so that the answers are always between 0 and 25. The solution? A modular system! Here’s a new rule:
To get the ciphered letter, add three to the original letter or “plaintext,” then take the remainder when you divide by 26. In symbols, this is: C = P + 3 (mod 26).
Problem D8
Decipher this message, which was created using Caesar’s code. Explain how you did it. Note 11

Problem D9
Here’s a new rule:
C = 3P + 2 (mod 26)
Use this rule to encipher a secret word (at least five letters long) for a partner. Note 12
Problem D10
Trade words with your partner and decipher their secret rule. Explain how you did it.
Problem D11
Can you find a rule that would undo this cipher? That is, can you find a and b so that P = aC + b (mod 26) is an equation that “undoes” C = 3P + 2 (mod 26)?
Modular systems for enciphering messages are not just for fun and games. It’s essential that a secret message be hard to decipher if you’re not the intended recipient, but easy to decipher if you are the intended recipient. Algorithmic ciphers are much better than “code books” because people can remember the algorithm, so it can’t be lost or stolen.
Modern cryptography, based on these modular systems — using blocks of letters instead of single letters, exponential functions, and very large prime numbers — is what’s used these days to keep your credit card number safe when you purchase something on the Internet!
Video Segment
In this video segment, Ari Juels of RSA Security describes the methods and applications of modular arithmetic to modern cryptography.
You can find this segment on the session video, approximately 21 minutes and 32 seconds after the Annenberg Media logo.
Note 7
One of the interesting extensions of these algebraic systems is the connection to equation solving. Many of the techniques for solving equations become automatic with experience, and solving equations in modular systems (mod 10 is the modular system for units digit arithmetic) draws attention to the properties of numbers that are sometimes assumed or taken for granted. For example, in solving 3x = 8, we need to determine whether or not 3 has an inverse in the system we’re dealing with.
Groups: Write 3x = 8 on an overhead, and discuss in a full group how you might solve this equation in units digit arithmetic. Some may say you should divide by 3; others may say you should multiply by 1/3. Remember that the only operations we have in our system are addition and multiplication, and 1/3 is not in the domain of units digit arithmetic. In fact, you need to consider what number is the reciprocal of 3 in our new system. If you have trouble, you can look at the table to see what number multiplied by 3 yields 1. Then go through the steps to solve the equation.
Groups: Next, write x + 4 = 2 on an overhead, and discuss how to solve this equation by adding the opposite of 4 to both sides.
Note 8
Groups: Work on Problems D1-D4 in small groups. You may notice that in mod 10, there are certain numbers that don’t have reciprocals: all of the numbers that share a factor with 10. (Another way to say this is: The only numbers that do have reciprocals are relatively prime to 10.) You may also want to take time to discuss how solving equations in units arithmetic differs from solving equations in the real number system.
Note 9
Working in different algebraic systems has applications not just inside mathematics, but in other fields as well. In this part, we’ll explore an applied use of modular systems. We’ll see how modular systems are helpful when you want to keep the answers to calculations within a certain range (in this case, the alphabet).
Note the meaning of the terms “plaintext” (the original message; it’s just the English words) and “ciphertext” (the encoded message; it looks like nonsense). Caesar reportedly used a very simple cipher to send military secrets: He assigned each letter a number from 0-25, then added 3 to the letter in the plaintext to get the ciphertext.
Note 10
Use the “letter tables” to work on Problems D6 and D7.
Groups: After thinking about how to encipher a “Y” with Caesar’s rule, have a discussion about how modular systems keep the results of calculations within a certain range. In the case of mod 10, all the answers were 0-9 (that is, units digits). If you want the answers to be between 0-25, you should work modulo 26, or just mod 26.
Groups: Put Caesar’s modified cipher on an overhead:
C = P + 3 (mod 26)
Note 11
Groups: Work on Problem D8 alone or with a partner. You may find that even though you know the rule, you will work on this as a “cryptogram,” making guesses and trying to see words. Explain your strategy to the group (usually looking at the letter table and subtracting 3 from each letter in the coded message).
Once you have a modular system, there’s no reason to restrict yourself to the rule “add 3.” You can perform any algebraic rule before using mod 26, and you’ll still get a cipher. (Some ciphers are better than others, though. Working mod 26, if you multiply by an even number or by 13, you will have several plaintext letters map to the same ciphertext letters. This is no good, because the cipher can’t be “undone,” even by its intended recipient! The reasons for this are beyond the scope of this course. We have stayed with multiples that create good ciphers.)
Note 12
Groups: Work on Problems D9-D11 with a partner. Problem D11 is quite challenging, and you may approach it any number of ways, either by using “data” from their secret words, or by trying to solve the equation for P.
Remember that there is no “divide by 3” rule in a mod 26 system. If you come up with the equation P = (C – 2) / 3 (mod 26), how would you decipher M? M = 12, so P = (12 – 2) / 3 = 10 / 3. How can you find 10 / 3 in this system?
Groups: Before wrapping up this part of the session, share your equations and solutions. If no one actually solved the equation for P, you can look at this solution on an overhead or on the board:
C = 3P + 2 (mod 26)
C – 2 (mod 26) = 3P (mod 26)
Notice that we need mod 26 on both sides at this point, because although C is between 0 and 25, C – 2 may not be (it may be -2, for example).
Now you need to multiply both sides of the equation by the reciprocal of 3. There is no 1/3 in a mod 26 system, but there is a number r, so that 3r = 1 (mod 26). Discuss what that number must be (the answer is 9, because 3 * 9 = 27 = 1 (mod 26)).
9 * (C – 2) (mod 26) = 9 * (3P) (mod 26)
P = 9 * (C – 2) (mod 26)
If you worked on this another way, you may have come up with different but equivalent equations:
P = 9 C – 18 (mod 26)
P = 9 C +12 (mod 26)
and so on.
Problem D1
First, add the opposite of 5 to both sides. This is 5, because 5 + 5 = 0. Then:
| • | 7x + 5 = 9 |
| • | 7x + 5 + 5 = 9 + 5 |
| • | 7x + 0 = 4 |
| • | 7x = 4 |
Now, we need to multiply by the reciprocal of 7. This is 3, because 7 * 3 = 1. Then:
| • | 7x = 4 |
| • | 3(7x) = 3 * 4 |
| • | (3 * 7)x = 2 |
| • | x = 2 |
This method will be effective, so long as the opposite of our added number exists, and so long as the inverse of our multiplied number exists.
Problem D2
Follow the same procedure as in Problem D1. The opposite of 7 is 3, and the reciprocal of 3 is 7. The answer is x = 9.
Problem D3
Since the opposite of 1 exists (it’s 9), we get 4x = 8. But 4 doesn’t have a reciprocal! The next step is to look through the multiplication table, trying to find any numbers that, when multiplied by 4, produce 8. There are two: x = 2 and x = 7. These are the two solutions. This means that a linear equation in the system of units digit arithmetic can have more than one solution.
Problem D4
Since 4 does not have a reciprocal, we need to use the table to find all solutions to 4x = 7. No such solution exists!
Problem D5
If A has an inverse, then there will be exactly one solution. If A does not have an inverse, then the number of solutions depends on the common factors of A and B. If A has no inverse and A and B do not have a common factor, then there will be no solutions. If A has no inverse and A and B do have a common factor, then there will be more than one solution. Specifically, the number of solutions will be two if A and B have 2 as a common factor and five if A and B have 5 as a common factor.
Problem D6
MDQH GRH is one possible solution.
Problem D7
Wrap around: Y + 3 = B. This works partially because B has been vacated by moving the rest of the alphabet forward.
Problem D8
“Undo” the steps by moving everything backwards 3 letters. The result is “Some people think that mathematics is a serious business that must always be cold and dry; but we think mathematics is fun and we aren’t ashamed to admit the fact.” The origin of the quote you have deciphered is a wonderful book called Conrete Mathemtics by Graham, Knuth, and Patashnik.
Problem D9
An example: CODES becomes KUNQG.
Problem D10
One way to do this is to build a table of plaintext and ciphertext, then decode using the table (like a decoder ring). For example, this table tells you that C becomes K, so if you are given ciphertext letter K, you know the original letter was C.
Problem D11
The rule requires you to “undo” the operations, solving for the variable P (since P is the original letter).
| • | C = 3P + 2, so we’ll “undo” the 2 by adding its opposite, which is 24 (2 + 24 = 0 in mod 26) |
| • | C + 24 = 3P + 2 + 24 |
| • | C + 24 = 3P (mod 26) |
Now, we’ll “undo” the 3 by finding its reciprocal, a number which makes 3R =1 in mod 26. This number is not too hard to find, since “1” is the same number as 1 + 26 = 27. This means R = 9 is the reciprocal.
| • | C + 24 = 3P |
| • | 9(C + 24) = 9(3P) |
| • | 9C + (9 * 24) = (9 * 3)P |
9C + 8 = P is the rule. Try it to see if it changes KUNQG into CODES