Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
Classroom Case Studies, Grades 6-8 Part D: More Problems That Illustrate Algebraic Thinking (25 minutes)
Session 10: 6-8, Part D
At the 6-8 grade level, there are many problems that prepare students for their later work in algebra. There is some evidence that more students are, in fact, taking a formal course in algebra in the eighth grade. The problems included in this session, however, may be used in courses both before and during students’ first formal course in algebra. Note 7
For each of the problems below, answer the following questions:
| a. | What algebraic content is in the problems? |
| b. | What content does it prepare students for later? |
| c. | How does this content relate to the mathematical ideas in this course? |
| d. | How would your students approach this problem? |
| e. | What are other questions that might extend students’ thinking about the problem? |
| f. | Does your current program in mathematics at your school include problems of this type? |
Problems
Problem D1
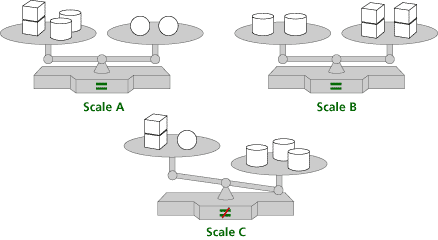
| a. | Which block, cylinder, sphere, or cube will balance Scale C? |
| b. | List or draw the steps you followed to identify the block. |
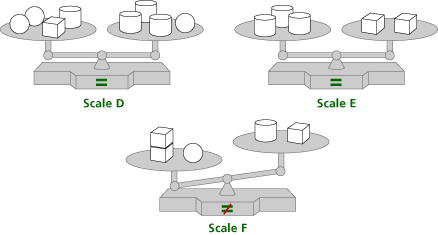
| c. | Which block, cylinder, sphere, or cube will balance Scale F? |
| d. | List or draw the steps you followed to identify the block. |
Problem D2
a. Find the weight of each block.
cylinder = ________ pounds
sphere = ________ pounds
cube = ________ pounds
b. Write or draw the steps you followed to solve the problem.
c. Find the weight of each block.
cylinder = ________ pounds
sphere = ________ pounds
cube = ________ pounds
d. Write or draw the steps you followed to solve the problem.
Problem D3
These signs tell about some items for sale. Same items have same prices. Different items have different prices. How much is:
| a. | A helmet? |
| b. | A bell? |
| c. | A bicycle lock? |
| d. | Explain how you figured out the prices. |
Problem D4
This is a staircase Deion built. He used 3 blocks for the 1st stair, 6 blocks for the 2nd stair, 9 blocks for the 3rd stair, and so on, using 3 more blocks for each higher stair.
| a. | Make a three-column table. In Column 1 show the Stair Number. In Column 2 show Number of Blocks used. In Column 3 show the Total Number of Blocks used to build the stairs from Stair 1 up to and including Stair 5. For example, for stairs 1-3, Deion used a total of 3 + 6 + 9, or 18, blocks. |
| b. | Let S represent the stair number, and let N represent the number of blocks. Complete this function rule to show the number of blocks needed to build Stair S. N = ? |
| c. | What is the number of blocks Deion would need to build Stair 10? |
| d. | Explain your answer to the above question. |
Problem D5
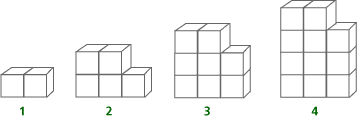
This is a series of growing shapes. Imagine that the building pattern continues. How many blocks will it take to build:
| a. | Shape 8? |
| b. | Shape 12? |
| c. | Tell in words how you would build Shape 5. |
| d. | Write a function rule to relate the number of blocks in a shape to the shape number. Let N represent the shape number. Let B represent the number of blocks in a shape. B = ? |
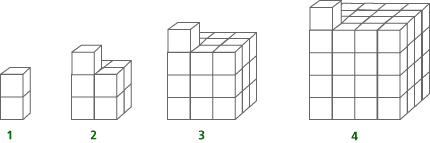
This is a series of growing cubes, with one small cube on top. Imagine the building pattern continues. How many blocks will it take to build:
| e. | Cube 7? |
| f. | Cube 20? |
| g. | Tell in words how you would build Cube 5. |
| h. | Write a function rule to relate the number of blocks in a cube to the cube number. Let N represent the cube number. Let B represent the number of blocks in a shape. B = ? |
Problems adapted from Groundworks: Algebraic Thinking, Grade 7, by Carole Greenes and Carol Findell (New York: Creative Publications, Wright Group/McGraw-Hill 1998).
The above material may not be reproduced without the written permission of Wright Group/McGraw-Hill.
Notes
Note 7
The problems in this section, while preparing students for work in more formal algebra courses, demonstrate more informal approaches to algebraic concepts, with respect to their contexts and the models they employ. Work on the problems from Groundworks,recording answers to questions (a)-(f) as you do each problem. It is important that you identify the mathematical content in each of the problems and how that content illustrates algebraic thinking.
Solutions
Problem D1
For the first set of scales the answer is 1 cube on the left pan. For the second set of scales the answer is 1 cylinder on the right pan
| a. | The mathematical content is balance, the notion that the objects on the lower pan on a pan balance weigh more than the objects on the higher pan, and that one object that balances with two or more objects is the heaviest. This prepares students for understanding equality as balance and the notion that adding or removing the same items from both sides of a balance retains balance. | ||||||||||||
| b. | This content introduces equality as balance, setting the stage for solving equations by manipulating them while maintaining balance. | ||||||||||||
| c. | This content illustrates methods for solving linear equations. | ||||||||||||
| d. | Students approach these problems in several ways:
|
||||||||||||
| e. | To extend students’ understanding, ask questions such as the following:
|
||||||||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D2
For the first set of scales the answers are: cylinder = 3, cube = 4,
sphere = 6, cone = 1.
For the second set of scales the answers are: cylinder = 5, cube = 1,
sphere = 2, cone = 4.
Possible responses to the questions to consider:
| a. | The mathematical content is the concept of variable and solving four equations in four variables. | ||||||
| b. | This content prepares students for understanding that they can replace a variable with its value. | ||||||
| c. | This content illustrates methods for solving systems of linear equations. | ||||||
| d. | Students approach these problems in several ways. One way is shown for each problem.
|
||||||
| e. | To extend students understanding, ask them to describe other ways to solve the problems and ask questions, such as the following about the first set of scales:
|
||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D3
Answer: helmet = $29, bell = $10, lock = $24
Possible responses to the questions to consider:
| a. | The mathematical content is the concept of variable and solving three equations in three variables. | ||||||||
| b. | This content prepares students for understanding that they can replace a variable with its value. | ||||||||
| c. | This content illustrates methods for solving systems of linear equations. | ||||||||
| d. | Students approach these problems in several ways. Two ways are shown.
|
||||||||
| e. | To extend students’ understanding, ask questions such as the following:
|
||||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D4
Answers: 1, 3, 3; 2, 6, 9; 3, 9, 18; 4, 12, 30, 5, 15, 45
The rule for the number of blocks for stair N is N = 3S, so for Stair 10 it takes 3 * 10, or 30 blocks.
Possible responses to the questions to consider:
| a. | The mathematical content is function. |
| b. | This content prepares students for making tables of values to represent data and for writing functions from those tables. |
| c. | This content illustrates the representation of a function as a scenario, a table of values, and an equation. |
| d. | Students approach these problems in several ways. One way is shown here. Each stair requires 3 more blocks than the prior stair. The 1st stair requires 3 blocks, the 2nd stair requires 2 * 3 blocks, the 3rd stair requires 3 * 3 blocks, so the Sth stair will require 3 * S blocks. |
| e. | To extend students’ understanding, ask them to find the rule for the total number of blocks (T) needed to build S stairs. (That rule is T = (3 / 2)S(S + 1).) |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem D5
For the first set of shapes the rule is B = 2 + 3(N – 1) = 2N + (N – 1) = 3N – 1
For the second set of shapes the rule is B = 1 + N3
Possible responses to the questions to consider:
| a. | The mathematical content is inductive reasoning and writing functions. | ||||||
| b. | This content prepares students to identify, continue, and generalize patterns. | ||||||
| c. | This content illustrates the difference between linear and nonlinear functions. | ||||||
| d. | Students approach these problems in several ways. One way is shown here:
|
||||||
| e. | To extend students’ understanding, ask questions such as the following:
|
||||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
