Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Suppose you are given two different options for salary at a temporary job. Note 5
| Plan A: | You can earn $2,000 each week, or |
| Plan B: | You can earn 1 penny the first week, 2 pennies the next week, 4 pennies the next week, and so on, doubling your salary each week. |
The job lasts 25 weeks, and your goal is to earn the largest total salary for the 25 weeks.
Which salary plan would you choose and why? Write down your initial reaction.
Use a spreadsheet or some other method to figure out which salary plan is better.
Tip: When using a spreadsheet, create three columns, one for the week number, one for plan A, and one for plan B. When creating the rule for plan B, remember that the salary is doubling each week, and that the first week’s salary is one penny, not one dollar.
Are you surprised that the second salary grew so rapidly? Use the spreadsheet to determine how much money you would make from plan B in 40 weeks.
Tip: To make a column wider, click and hold down on the right edge of the column heading letter, then drag the mouse to the right.
| Video Segment
In this video segment, on screen participants discuss the differences between salary plans A and B in Problems B1 and B2 above. In particular, they explore the differences between linear and exponential functions. Watch this segment after you have worked on Problems B1 and B2. If you get stuck, you can watch the video segment to help you. Describe the difference in the ways salary plans A and B grow. Which one is a proportional change, and which is an absolute change? For more on this, see Session 4, Part A. You can find this segment on the session video, approximately 7 minutes and 51 seconds after the Annenberg Media logo. |
Many populations — human, plant, and bacteria — grow exponentially, at least at first. In time, these populations start to lose their resources (space, food, and so on).
Note 6
Here’s an example:
“Whale Numbers up 12% a Year” was a headline in a 1993 Australian newspaper. A 13-year study had found that the humpback whale population off the coast of Australia was increasing significantly. The actual data suggested the increase was closer to 14 percent!
When the study began in 1981, the humpback whale population was 350. Suppose the population has been increasing by about 14 percent each year since then. To find an increase of 14 percent, you could do either of the following (P stands for population):
Pthis year = Plast year + (0.14) * Plast year
Pthis year = (1.14) * Plast year
Each of these is a recursive rule. The first rule says that to know this year’s population, start with last year’s population (which is Plast year), then add the population growth. Since the growth is 14 percent of last year’s population,
add (0.14) * Plast year.
The second rule is used more frequently because it’s easier to calculate — it incorporates the adding in one calculation. This equation shows that the second computation is equivalent to the first:
x + (0.14) * x = (1.14) * x
The second computation fits the format of an exponential function, because successive outputs have the same ratio (in this situation, the ratio is 1.14).
Problem B4
Make a table that shows the estimated whale population for the 5 years after 1981.
Note 7
| Years after 1981 | Estimated Population | |
| 0 | 350 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Problem B5
If the whale population continues to grow by 14 percent per year, predict how many whales there would be in 2001 (20 years after 1981).
Tip: See if you can do this problem without extending your table from Problem B4. You would need to use a closed-form rule to “jump” directly to the 2001 answer.
Problem B6
How many years does it take the whale population to double if it grows at this rate? Does your answer depend on the starting value of the whale population?
|
Video Segment In this video segment, taken from the “real world” example at the end of the Session 7 video, Mary Bachman of the Harvard School of Public Health discusses the exponential model of population growth, the factors that affect the model, and the uses of population modeling. Do you think the whale population discussed in Problems B3-B6 could increase at 14 percent per year forever? Why or why not? You can find this segment on the session video, approximately 22 minutes and 40 seconds after the Annenberg Media logo. |
Problem B7
Look at the following toothpick pattern. The number of toothpicks needed to build each stage of the pattern is a linear function. Note 8

Create a toothpick pattern in which the number of toothpicks you need for each stage is an exponential function.
Tip: Think of a pattern that would require you to double the number of toothpicks you use at each step. That would form an exponential function, because successive outputs have a common ratio (2).
Note 5
In this section, we’ll explore situations that give rise to increasing exponential functions.
Groups: Begin by putting up an overhead of the description of two different salary options for Problems B1 and B2. Discuss your gut reactions: Which is the better choice? No need to justify your answers; go instead with your first instincts.
Work with a spreadsheet or calculator to figure out the final value of each salary scenario. Remember that the most important factor in this comparison is the total amount earned over the 25 weeks.
A calculator can be used to create the same table as in a spreadsheet. Even if you are filling in the table by hand, there are shortcuts to using the calculator. For example, type in “.01” then “Enter.” Then type “x 2” and “Enter.” Repeatedly hitting the Enter key will produce the list of outputs for the second salary option. Keep track of each output, and then sum the outputs at the end. For the first salary option, because the salary never changes, simply multiply the salary ($2,000) by the number of weeks (25) to get the total.
Groups: When finished the comparison, share your results and reactions. Many will probably be surprised that starting with such a small amount — a penny compared with $2,000 — you could end up with more than 10 times as much total money, and in only half a year.
Note 6
The salary activity segues nicely into the population model. If a population reproduced by doubling, it would quickly run out of resources, even starting with a small number. Though exponential models are used for some populations, the bases (the constant multiple between outputs) is usually much closer to 1.
Groups: Read through the whale problem. Spend a moment discussing why increasing by 14 percent is mathematically equivalent to multiplying by 1.14. Percents are not a focus of this session, but it’s worth spending a little time on this idea in order to understand why it is true. You can also relate it to other things the students probably know:
These are specific cases of an important algebraic idea: the distributive property of multiplication over addition.
Here, we have
1 x (population) + 0.14 x (population) = (1 + 0.14) x (population) = 1.14 x (population)
Note 7
If working on a computer, open a new worksheet to model the situation.
Groups: Work in pairs on Problems B4-B6.
Think about a strategy for calculating how long the population takes to double. The Fill Down command on the spreadsheet can be used until a population of 700 is reached. To answer the question of whether it depends on the initial population, change that starting number in the spreadsheet and see if it doubles in the same place. The doubling time does not depend on the starting value; thus an exponent n can be found so that 1.14n = 2.
Here’s one way to see that the time to double doesn’t depend on the starting value, and it also highlights some important algebraic thinking.
|
||||||||||||||||||||||||||||||||||||
You’re looking for a year where 1.14 x 1.14 x 1.14x … x 1.14 x n = 2 x n. There is an n multiplied on each side, so the only thing that could possibly make the multiple of 2 is all those 1.14s multiplied together. You just have to find the right number of them, and the number of 1.14s only depends on the year.
This also tells you that, for example, if you get a 5 percent raise at your job every year, the number of years it takes you to double your salary is fixed, and it doesn’t depend on how much you start out earning.
Note 8
Groups: Problem B7 relates back to earlier work with toothpick patterns, but requires a bit of creativity. You may want to have actual toothpicks available. If you have difficulty coming up with patterns that work, think of a particular case. For example, try to come up with a pattern that uses twice as many toothpicks at each successive stage. To maintain a pattern visually, it helps to think about making copies of the shape at any stage, and arranging them in some regular way.
Here are a couple of possible solutions:


Groups: To wrap up this part, talk about how “growing exponentially” is used as slang in the press to mean “growing very fast,” but in fact “exponentially” has a specific mathematical definition. Think of possible definitions for “growing exponentially” in your own words, and add exponential functions to the list of nonlinear functions started at the beginning of the session.
Problem B1
Most initial reactions are to choose plan A.
Problem B2
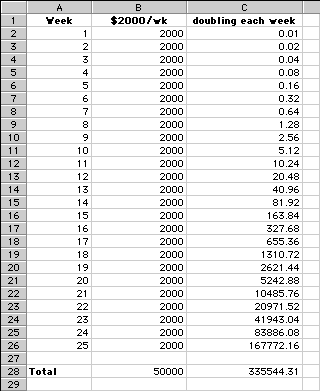
The total for 25 weeks of plan A, at $2,000 per week, is $50,000. Plan B, which starts at 1 penny and doubles each week totals $335,544.31, including $167,772.16 in the final week.
Problem B3
After 40 weeks, the grand total at this job would be $10,995,116,277.75, including just under $5.5 billion in the last week. Before the end of the year, you would exhaust the total money supply of the United States.
Problem B4
Here is the completed table.
|
Problem B5
You can extend the spreadsheet, but an easier way to obtain an answer would be to calculate 350 * (1.14)20 = 4,810 whales. One way to estimate this is to observe that the population seems to be nearly doubling in 5 years (doubling would be 700 whales). This means that we could expect the population to nearly double three more times in a total of 20 years. This doubling would be 350 -> 700 -> 1,400 -> 2,800 -> 5,600, so an estimate is roughly 5,000 whales.
Problem B6
It takes a little more than 5 years. And no, it doesn’t matter what the initial population value was, because the ratio of the population after 5 years from now relative to starting population is created only by multiplying 1.14 five times.
Problem B7
One possible pattern is to build, at each stage, a triangle of toothpicks with sides twice as long as the previous triangle.
