Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Look at this table:
| Input | Output |
| 1 | 6 |
| 2 | 10 |
| 3 | 14 |
| 4 | 18 |
| 5 | 22 |
| 6 | 26 |
| ? | ? |
| ? | ? |
Mr. Lewis looked at the table in Problem H1 and said, “Oh, I get it. Just do these steps.”
If you do all this, you’ll get the numbers in the table.” Does Mr. Lewis get it? Does Mr. Lewis’ method agree with yours for the first three outputs? For the next three? Which method is correct?
A frog climbs up the side of a well and slides back while resting. Every minute the frog leaps forward 5 meters (and it leaps forward precisely at the end of the minute). Then it rests for a minute. At the end of the rest, the frog slips back 3 meters. At the end of the next minute it leaps (5 meters), then a minute later it slides back (3 meters), and so on.
Here is a picture of a well 11 meters deep.
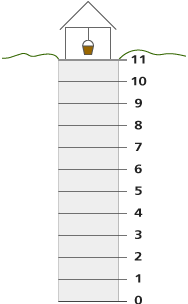
You may find it helpful to work with someone to model what’s happening in the problem.
Vance, James. “Number Operations from an Algebraic Perspective.”
Reproduced with permission from Teaching Children Mathematics, © 1998 by the National Council of Teachers of Mathematics. All rights reserved.
Solomon, Jesse, Carol Martignette-Boswell, et al. “Toward a Cooperative Model of Math Staff Development.”
Reproduced with permission from Mathematics Teaching in the Middle School, © 1997 by the National Council of Teachers of Mathematics. All rights reserved.
Download PDF File:
Chapter 1
Chapter 2
Usiskin, Zalman. “Conceptions of School Algebra and Uses of Variables.”
Reproduced with permission from The Ideas of Algebra, Grades K-12: 1988 NCTM Yearbook, © 1988 by the National Council of Teachers of Mathematics. All rights reserved.
Download PDF File:
Chapter 1
Chapter 2
Problem H1
Problem H2
Mr. Lewis is making things a lot more difficult than they need to be! Here’s the analysis on the number n:
| Input(n) | Output(n2 + 1) | Mr. Lewis’s Rule |
| 1 | 2 | 6 + 6 – 10 = 2 |
| 2 | 5 | 24 + 6 – 25 = 5 |
| 3 | 10 | 54 + 6 – 50 = 10 |
| 4 | 17 | 96 + 6 – 90 = 12 |
| 5 | 26 | 150 + 6 – 150 = 6 |
| 10 | 101 | 600 + 6 – 1750 = -1144 |
As you can see from the table, Mr. Lewis’s rule generates the three numbers we were given in the table, but begins to veer away from the table’s values quickly. By n = 10 there is a drastic difference in the values from the two rules. This doesn’t make Mr. Lewis’s rule wrong, but it is definitely not the simplest rule that generates the table’s values.
Problem H3
| Height of well | Time it takes to get out |
| 1 | 1 minute |
| 2 | 1 minute |
| 3 | 1 |
| 4 | 1 |
| 5 | 3 |
| 6 | 3 |
| 7 | 5 |
| 8 | 5 |
| 9 | 7 |
| 10 | 7 |
| 11 | 9 |
| 12 | 9 |
| 13 | 11 |
| 14 | 11 |
| 15 | 13 |
| 16 | 13 |
| 17 | 15 |
Three observations: First, the values are all 1 minute until the well is 6 meters deep, because the frog can climb 5 meters in the 1st minute. Second, the times to climb out are all odd numbers, because it takes 2 minutes before the frog will climb again. Third, the times occur in pairs, because the difference between the frog’s jumping distance and sliding distance is 2 meters. This means that it won’t matter if the frog needs to make 6 meters or 7 meters, because it will make either in 2 jumps.
Problem H4
This means that we’ll need to calculate (H – C) / (C – S) to find how many 2-minute cycles the frog will need to go through to get within C meters of the top, then 1 more minute to escape. Additionally, because (H – C) / (C – S) often gives a fraction, we have to include instructions to round that number up to the next integer. (This is usually called the “ceiling” function, and is denoted by the oddly shaped brackets seen below. We used this function when we talked about Eric the Sheep.) Additionally (!), because (H – C) might be negative, we have to make an exception for those times that the frog can just hop on out. So, having done all that, here’s the formula for T, the time that it takes the frog to escape:
![]()
Test it out on the previous problems if you like.