Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In This Part:
At the K-2 grade level, there are many problems that prepare students for their later work in algebra. Experiences with these problems can also build bridges between arithmetic and algebra, while increasing the students’ chances for success in future mathematics.
In this section we’ll analyze problems at the K-2 level for their algebraic content. For each K-2 problem, find a mathematical solution, then answer questions (a)-(f) listed below. If it is helpful, print this page and refer to the questions as you work on each problem.
a. What algebraic content is in the problems?
b. What content does it prepare students for later?
c. How does this content relate to the mathematical ideas in this course?
d. How would your students approach this problem?
e. What are other questions that might extend students’ thinking about the problem?
f. Does your current program in mathematics at your school include problems of this type?
Problem C1
Draw two strips with this pattern
![]()
| a. | How many X’s are in the two strips all together? |
| b. | How many +’s are in the two strips all together? |
| c. | Predict how many O’s will be in four strips all together. |
| d. | How do you know? |
| e. | Draw the strips to check. |
| Now draw four strips with this pattern: |
![]()
| a. | How many X’s are in the four strips all together? |
| b. | How many O’s are in the four strips all together? |
| c. | Predict how many X’s will be in six strips all together. |
| d. | How do you know? |
| e. | Draw the strips to check. |
Problem C2
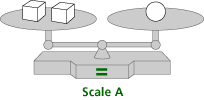
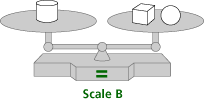
For each scale, determine which weighs more — the cube, the cylinder, or the sphere — and explain how you know.
Which scale has the heavier blocks? Explain how you know.
For each K-2 problem, find a mathematical solution, then answer questions (a)-(f) listed below. If it is helpful, print this page and refer to the questions as you work on each problem.
| a. | What algebraic content is in the problems? |
| b. | What content does it prepare students for later? |
| c. | How does this content relate to the mathematical ideas in this course? |
| d. | How would your students approach this problem? |
| e. | What are other questions that might extend students’ thinking about the problem? |
| f. | Does your current program in mathematics at your school include problems of this type? |
Problem C3
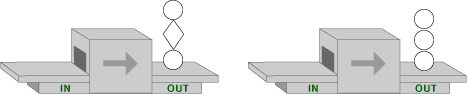
Notice the pattern in these two machines:

These machines below work in the same way. What goes into the machines? What comes out of them? Describe what each machine does.

Problem C4
Notice the pattern in these two machines:

These machines below work in the same way. What goes into the machines? What comes out of them? Describe what each machine does.


For each of the following problems, answer the questions below:
| a. | What algebraic content is in the problems? |
| b. | What content does it prepare students for later? |
| c. | How does this content relate to the mathematical ideas in this course? |
| d. | How would your students approach this problem? |
| e. | What are other questions that might extend students’ thinking about the problem? |
| f. | Does your current program in mathematics at your school include problems of this type? |
Problem C5
Notice the pattern in these two machines:

These machines below work in the same way. What goes into the machines? What comes out of them? Describe what each machine does.


Problem C6
Notice the pattern in these two machines:

These machines below work in the same way. What goes into the machines? What comes out of them? Describe what each machine does.


For each of the following problems, answer the questions below:
| a. | What algebraic content is in the problems? |
| b. | What content does it prepare students for later? |
| c. | How does this content relate to the mathematical ideas in this course? |
| d. | How would your students approach this problem? |
| e. | What are other questions that might extend students’ thinking about the problem? |
| f. | Does your current program in mathematics at your school include problems of this type? |
Problem C7
Notice the pattern in these two machines:

For each of the number machines below describe what goes in or what goes out, then explain how the machine works.




For each of the following problems, answer the questions below:
| a. | What algebraic content is in the problems? |
| b. | What content does it prepare students for later? |
| c. | How does this content relate to the mathematical ideas in this course? |
| d. | How would your students approach this problem? |
| e. | What are other questions that might extend students’ thinking about the problem? |
| f. | Does your current program in mathematics at your school include problems of this type? |
Problem C8
Notice the pattern:

What comes out?
What goes in?
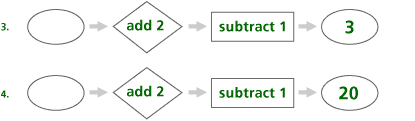
Explain what the hexagon does.
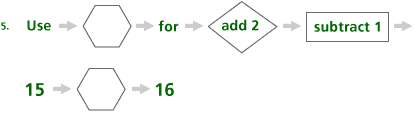
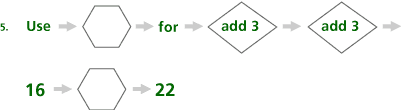
Problem C9
Notice the pattern:

What comes out?
What goes in?
Explain what the hexagon does.
Note 6
It is often difficult for teachers to see how the mathematics content at their grade level builds algebraic thinking. Therefore, it is important to look at many examples of elementary mathematics that build bridges to algebraic thinking.
Groups: Work on the problems from Groundworks, recording answers to questions (a)-(f) as you do each problem. In Problem C1, the goal is for students to predict and verify the numbers of characters in a pattern. Some questions to ask, as suggested by the authors, include:
| • | What is the pattern? |
| • | How many Xs are in the pattern? |
| • | How many Os are in the pattern? |
| • | What will you draw in the first box? Second box? Third box? Fourth box? Fifth box? |
You may think that your students will have difficulty predicting the character in each box without filling in the entire strip. Students should be encouraged to find ways of predicting without having to do the filling first.
In Problem C2, the goal is to recognize that a balance scale in essence represents equality. Some questions the authors suggest are:
| • | What does Scale B show? |
| • | In Scale A, what blocks are in the left pan? In the right pan? |
| • | In Scale A, which pan is heavier? |
In Problem C3 and C4, the goal is to figure out the function rule from the example, and then to apply the rule to determine the output when given the input, and the input when given the output. Students are also asked to find a rule that describes what the machine does.
Some questions the authors suggest include:
| • | What shape went into the first machine? |
| • | What shape came out of the first machine? |
| • | What shape went into the second machine? |
| • | What shape came out of the second machine? |
| • | What is alike about the two figures that came out? |
In Problem C5-C7, the goals are the same as Problem C3. Some questions suggested by the authors are:
| • | Look at the first example. What number goes in? What number comes out? |
| • | Look at the second example. What number goes in? What number comes out? |
| • | What do you think the machine is doing? |
Students may find it useful to act out what is happening in these machines.
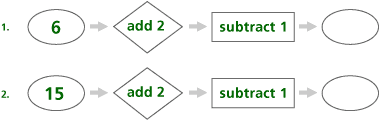
In Problem C8 and C9, the goal is to apply the function rules to determine the output when given the input, the input when given the output, and also to describe the rule.
Questions to ask, as suggested by the authors, include:
| • | What number goes into the stepper first? |
| • | What does the first part of the stepper do to the number? |
| • | What does the second part of the stepper do to that number? |
| • | What is the final result? |
Problem C1
| a. | The mathematical content is patterns and proportional reasoning. | ||||||||
| b. | This prepares students for reasoning with proportions, predicting how many of a particular item will be in a strip of a given length, and using drawings to help solve problems. | ||||||||
| c. | This content requires the use of proportional reasoning and all the skills related to patterns: finding, describing, explaining, and using patterns to predict. | ||||||||
| d. | Students could approach these problems in several ways:
|
||||||||
| e. | To extend students’ understanding, ask questions such as the following:
|
||||||||
| f. | Very few textbooks contain problems of this type. |
Problem C2
| a. | The mathematical content is balance, the notion that the objects on the lower pan on a pan balance weight more than the objects on the higher pan, and that one object that balances with two objects is the heaviest of the three objects. | ||||
| b. | This prepares students for understanding equality as balance. | ||||
| c. | This content introduces equality as balance to set the stage for solving equations by manipulating equations while maintaining balance. | ||||
| d. | Students might use the following reasoning to solve this problem: Since Scale B has both a cube and a sphere on one side, and Scale A has only a sphere on one side, Scale B must have heavier blocks. | ||||
| e. | To extend students’ understanding, ask students to describe other ways to solve the problem or to make up weights for each block that would preserve the balance, and ask questions such as the following:
|
||||
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem C3
| a. | The mathematical content is function as a machine that takes one input, does something to that input, and returns exactly one output. |
| b. | This prepares students for understanding function. |
| c. | This content gives students an intuitive understanding of function. By using the machine metaphor and choosing shapes rather than numbers, students realize that you must get exactly one output for every input, thus gaining an intuitive understanding of function. |
| d. | Students approach these problems by examining and comparing the given inputs and outputs and describing what is the same and what is different in each case. |
| e. | To extend students’ understanding, ask them to make their own shape machines. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem C4
| a. | The mathematical content is function as a machine that takes one input, does something to that input, and returns exactly one output. |
| b. | This prepares students for understanding function. |
| c. | This content gives students an intuitive understanding of function. By using the machine metaphor and choosing shapes rather than numbers, students realize that you must get exactly one output for every input, thus gaining an intuitive understanding of function. |
| d. | Students approach these problems by examining and comparing the given inputs and outputs and describing what is the same and what is different in each case. |
| e. | To extend students’ understanding, ask them to make their own shape machines. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem C5
| a. | The mathematical content is function as a machine that takes one input, does something to that input, and returns exactly one output. |
| b. | This prepares students for understanding function. |
| c. | This content gives students an intuitive understanding of function. These machines extend students understanding of function by using numbers as inputs and outputs. |
| d. | Students approach these problems by examining and comparing the given inputs and outputs and describing what is the same and what is different in each case. |
| e. | To extend students’ understanding, ask them to make their own number machines. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
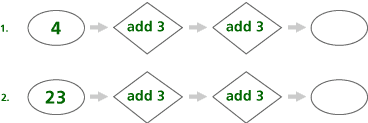
Problem C6
| a. | The mathematical content is function as a machine that takes one input, does something to that input, and returns exactly one output. |
| b. | This prepares students for understanding function. |
| c. | This content gives students an intuitive understanding of function. These machines extend students understanding of function by using numbers as inputs and outputs. |
| d. | Students approach these problems by examining and comparing the given inputs and outputs, and describing what is the same and what is different in each case. |
| e. | To extend students’ understanding, ask them to make their own number machines. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
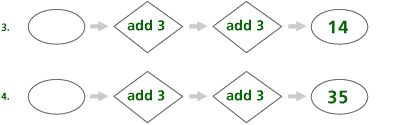
Problem C7
| a. | The mathematical content is function as a machine that takes one input, does something to that input, and returns exactly one output. |
| b. | This prepares students for understanding function. |
| c. | This content gives students an intuitive understanding of function. These machines extend students understanding of function by using numbers as inputs and outputs. |
| d. | Students approach these problems by examining and comparing the given inputs and outputs and describing what is the same and what is different in each case. |
| e. | To extend students’ understanding, ask them to make their own number machines. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem C8
| a. | The mathematical content is two-step functions depicted as a flow chart showing one input that goes through two operations and gives one output. |
| b. | This prepares students for understanding two-step functions. |
| c. | This content gives students an intuitive understanding of multi-step functions. These machines extend students understanding of function by using more than one operation. |
| d. | Students approach these problems by following the flow chart. Start with an In number, take it through the first operation, put that number through the second operation, and then write the Out number. |
| e. | To extend students’ understanding, ask them to make their own two-steppers. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |
Problem C9
| a. | The mathematical content is two-step functions depicted as a flow chart showing one input that goes through two operations and gives one output. |
| b. | This prepares students for understanding two-step functions. |
| c. | This content gives students an intuitive understanding of multi-step functions. These machines extend students understanding of function by using more than one operation. |
| d. | Students approach these problems by following the flow chart. Start with an In number, take it through the first operation, put that number through the second operation, and then write the Out number. |
| e. | To extend students’ understanding, ask them to make their own two-steppers. |
| f. | Answers will vary. Very few textbooks contain problems of this type. |