Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In This Part
Here’s a simple number puzzle that leads to a surprisingly challenging investigation. Note 3
It’s a hot summer day, and Eric the Sheep is at the end of a line of sheep waiting to be shorn. There are 50 sheep in front of him. Being an impatient sort of sheep, though, every time the shearer takes a sheep from the front of the line to be shorn, Eric sneaks up two places in line.
Problem B1
Without working out the entire problem, predict how many sheep will get shorn before Eric. Note 4
Problem B2
One way to help solve a complicated problem is to solve a smaller version of the same problem. In this activity, you will solve a version of Eric’s problem, one with a shorter line. Notice any patterns you find — they will help you understand and solve the larger problem.
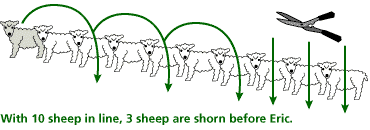
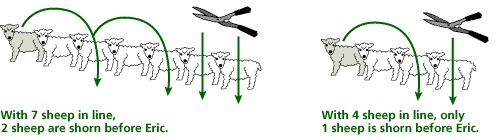
You can use counters, plastic chips, or coins to try out various smaller versions of this problem. Complete the following table:
| Number of sheep in front of Eric | Sheep shorn before Eric |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 |
Problem B3
Use the table from Problem B2 to predict how many sheep will get shorn before Eric if there are 50 in line in front of him.
Tip: Look for a pattern in the table, then extend it. Are you using algebraic thinking?
Problem B4
Describe the strategies you used to find the answer to Problem B3 and how you could predict the answer for any number of sheep in the line. Is your method for predicting “algebraic”? Why or why not?
| Video Segment
In this video segment, Professor Cossey and the participants discuss strategies for solving a problem with sheep shearing and then discuss the involvement of the number three in all the solutions. Were you surprised by the different ideas presented in solving this problem? Which of these ideas reflect algebraic thinking? You can find this segment on the session video, approximately 7 minutes and 21 seconds after the Annenberg Media logo. |
Problem B5
Work out the solutions for the boxes left blank in the table below:
| Number of sheep in front of Eric | Sheep shorn before Eric |
| 37 | |
| 296 | |
| 1000 | |
| 7695 | |
| 13 | |
| 21 |
Help: You will have to work backwards for the last two entries. Some problems may have more than one answer.
The Eric the sheep problem is from the Task Center Project, Curriculum Corporation, Australia.
Problem B6
Eric gets more and more impatient. Explore how your rule changes if Eric sneaks past 3 sheep at a time. How about 4 sheep at a time? 10 sheep at a time?
Problem B7
When someone tells you how many sheep there are in front of Eric and how many sheep at a time he can sneak past, describe how you could predict the answer.
Tip: A formula for the exact answer is very difficult to find here. “Describe” does not mean you must find an exact rule.
Problem B8
What if Eric sneaks past 2 sheep first, and then the shearer takes a sheep from the front of the line? Does this change your rule? If so, how?
Problem B9
The farmer hires another sheep shearer. There is still one line, but the 1st and 2nd sheep in line get shorn at the same time, then Eric sneaks ahead. Explore what this does to your rule.
Problem B10: Write and Reflect
There are several ways to represent a problem situation: as a written rule, in words or symbols, as a graph, as an equation, or as a table. What representation (or representations) did you use for Eric’s problem? Why did you choose those representations? Note 5
Problem B11
What reasoning skills did you use in the problems in Part B?
Note 3
The Eric the Sheep problem challenges us to describe patterns and use them to predict for large numbers of sheep. The problem is a good choice for this session because the pattern is more easily described in words than in symbols. Some people, however, may become frustrated that they can’t find a symbolic rule for describing the pattern. At this stage, it may be difficult to accept the notion that we’re thinking algebraically, even though we’re not using symbolic notation.
Groups: Begin the activity by having eight or nine people come to the front of the room. These people are sheep, and one of them, Eric, is at the end of a line waiting to be shorn. (Be sure to designate both an Eric and a sheep shearer.)
Here is the story: It’s a hot summer day, and all of the sheep are standing in line to be shorn. Eric is at the end of the line, and in this case there are __ sheep in front of him (as many as there are standing in line). But Eric is impatient, and every time the shearer takes a sheep from the front to be shorn, Eric then sneaks up the line 2 places. (Groups: Act this out. First move a sheep up to be shorn, then have Eric move up 2 places. It’s important that you sequence the shearing first, and then Eric moving up second.)
Then consider: How many sheep will be shorn before Eric? Guess the answer first, then act out the remaining steps.
Next, find some way of predicting how many sheep will be shorn before Eric if there are 50 sheep in front of him.
Note 4
Groups: Answer Problems B1-B9 in pairs or small groups.
It may be challenging to find the underlying function, which is a step function. It is important to reflect on what representations (table, graph, equation) were most helpful in thinking about how to predict down the line.
A typical answer to describing the function is, “Take the number of sheep in front of Eric, divide by 3, and round up.” This is a perfectly reasonable description, although some people may feel it is not as “legitimate” as a rule with symbolic notation. In fact, there is a way to represent this symbolically using the ceiling function notation:
![]() n
n![]() . This denotes the smallest integer greater than or equal to n. In the case of this problem, the number of sheep shorn before Eric would be
. This denotes the smallest integer greater than or equal to n. In the case of this problem, the number of sheep shorn before Eric would be ![]() n/3
n/3![]() , where n is the number of sheep in front of Eric. Do not focus on this notation, though. We don’t want the emphasis here to turn to symbolic notation.
, where n is the number of sheep in front of Eric. Do not focus on this notation, though. We don’t want the emphasis here to turn to symbolic notation.
It’s important to understand where the “three-ness” appears in the situation: 1 sheep is shorn, and Eric cuts in front of 2 sheep. Look at the three possible situations that Eric can be in when at the end of the line, and how they relate to the remainders when dividing by 3.
When we’re completing the table in Problem B5, we will have to work backwards for the last two entries. In fact, there are multiple answers for these because the function is not one-to-one.
The beauty of this problem is that it at first seems so simple, yet the extensions are quite challenging, even for sophisticated learners.
Note 5
Groups: Discuss Problems B10 and B11 as a whole group. Although everyone may not be aware of this, we are in fact choosing a representation to describe a real-world situation. Unfortunately, many problems that we have encountered do not give us a choice about representation.
Problem B2
Here is the completed table:
| Number of Sheep in front of Eric | Number of sheep shorn before Eric |
| 4 | 2 |
| 5 | 2 |
| 6 | 2 |
| 7 | 3 |
| 8 | 3 |
| 9 | 3 |
| 10 | 4 |
| 11 | 4 |
Problem B3
The table suggests that the number of sheep shorn before Eric goes up by 1 every three sheep, so there will be 17 sheep shorn before Eric if there are 50 in line ahead of him.
Problem B4
You might consider making a table, or looking for a pattern and giving a description like the one above. The description is “algebraic” if it involved mathematical thinking tools. It would not be algebraic if you decided to build the above table and continue it until you could read the answer.
Problem B5
Here is the completed table:
| Number of Sheep in front of Eric | Number of sheep shorn before Eric |
| 37 | 13 |
| 296 | 99 |
| 1000 | 334 |
| 7695 | 2565 |
| 37, 38, or 39 | 13 |
| 61, 62, or 63 | 21 |
Note that there is more than one answer to the last two questions (exactly three, actually). Also note that you need to think algebraically to answer the question for larger numbers.
Problem B6
If Eric sneaks ahead of 3 sheep at a time, the table will appear different: The number shorn before Eric will grow by 1 for every 4 sheep shorn (instead of 3). If he sneaks ahead of 10 sheep at a time, the number shorn before Eric grows by 1 for every 11 sheep shorn.
Problem B7
You could build a formula, or algorithm. One algorithm is to round up the number S / (k + 1), where S is the number of sheep in front of Eric, and k is the number of sheep he sneaks past each time. The “1” in this algorithm accounts for the 1 sheep shorn at the front of the line.
Problem B8
Because Eric sneaks past 2 sheep immediately, the rule becomes: Round up (S – 2) / (k + 1). Another possible rule is to round down S / (k + 1).
Problem B9
In this situation, two sheep are shorn each time before Eric sneaks up two sheep. We get the following table:
| Number of sheep in front of Eric | Sheep shorn before Eric | |
| 4 | 2 | |
| 5 | 3 | |
| 6 | 4 | |
| 7 | 4 | |
| 8 | 4 | |
| 9 | 5 | |
| 10 | 6 | |
| 11 | 6 | |
| 12 | 6 | |
| 13 | 7 |
So, the rule is: If the number of sheep in front of Eric is not two more than a multiple of 4 (e.g., 5, 7, etc.) divide the number of sheep in front of Eric by 2 and round up. If the number of sheep in front of Eric is two more than a multiple of 4 (e.g., 6, 10, 14, etc.), divide by 2 and add 1.
Problem B10
You may have used a graph, a table, or a description of the rule in words or algebraic symbols.
Problem B11
Reasoning skills would be used to make a convincing argument that the number 3 will be involved in the construction of a general rule for Eric the Sheep’s behavior, or to explain why the pattern will continue past the first 12 sheep.