Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Patterns, Functions, and Algebra
More Nonlinear Functions Part C: Different Functions (35 minutes)
Session 8, Part C
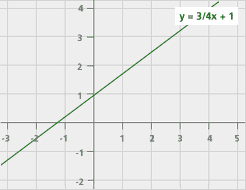
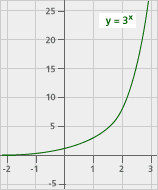
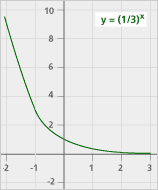
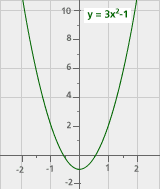
We’ve seen many different kinds of functions in the past few sessions. We’ve examined characteristics of functions, looked at their graphs, and explored situations where they arise. In general, people tend to think in terms of linear functions, trying to fit given data into lines. What we’ve seen, however, is that there are many other kinds of functions. Here are examples of their equations and graphs:
Note 8
| Linear Function y = ax + b |
Exponential Growth Function y = bx, where b > 1 |
|
 |
 |
|
| Exponential Decay Function y = bx, where b < 1 |
Quadratic Function y = ax2 + bx + c |
|
 |
 |
|
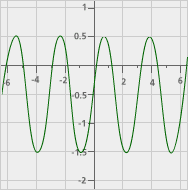
| Cyclic Function outputs repeat |
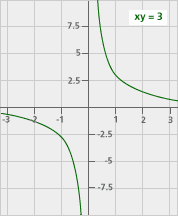
Inverse Proportion y = k / x, or xy = k |
|
 |
 |
|
It’s important to be familiar with various kinds of functions. Many different functions might fit just a few pieces of data. Here’s an example to show how this might happen.
Problem C1
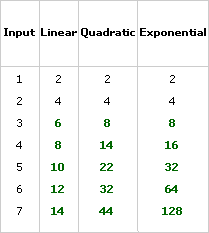
Fill in the missing entries according to the rules given above.
Problem C2
Here’s a picture of the three functions given above, showing how they share the same two points. A cyclic function also shares those two points.
Which function corresponds to which number?
Take It Further: Problem C3
How many different functions could fit these two data points, (1,2) and (2,4)? Explain your answer. Can you describe one other function that fits these two data points, either with an equation or through some other way? Note 9
Tip: Because there is only one line between two points, any different function would have to be nonlinear.
Notes
Note 8
The purpose of this section is to pull together ideas about functions from the past several sessions and to see how many different functions could fit a small set of data. Start by reviewing the different kinds of functions we’ve seen, both linear and nonlinear.
Some of the graphs look similar to each other, at least in places (exponential growth and the parabola, for example). Think about differences in these functions and how the graphs would differ from each other on a larger scale
Groups: Work on Problems C1-C3.
Note 9
Groups: Share answers to Problem C3, and see how many different functions — and how many kinds of functions — you’ve come up with.
Any linear function that answers the question in Problem C3 must be equivalent to the one given in the table. (For example, the expression 2 * (input + 1) – 2 works, but gives the same output everywhere as 2 * input, so it is the same function.) Through any two points (in this case, two input/output pairs) there is exactly one line, so any two linear functions that match those points must be equivalent.
Groups: Discuss the concepts outlined above.
Consider what quadratic functions could answer Problem C3. These are harder to come up with, but in fact there are an infinite number of quadratic functions that fit the two inputs given. The reason for this is subtle: You need two points to find exactly one line. You need three points to find exactly one parabola (quadratic function). Since there are only two points given, you can pick any third point. So you can pick an output for 3 and find a quadratic that works. Picking a different output for 3 will give a different quadratic. Here are just three others that fit the points given:
- 1 + n (n +1) / 2 (in other words, the outputs are each one more than the triangular number for that input)
- 5n – n2 – 2
- 2n2 – 4n + 4
Think about whether there are any other kinds of functions that fit the data. Note that a “height of tide” type function like that in Part A could also fit, and is a cyclic function. Here’s an example:
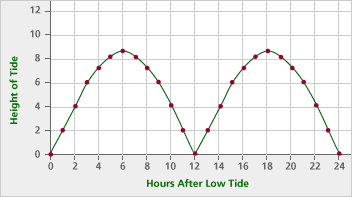
Groups: Consider making a poster of the four graphs together. It’s easy to see that you could sketch another function through those same two points that doesn’t match the other four functions given. In fact, you could sketch infinitely many different functions through those same two points. If you have trouble coming up with algebraic representations of the functions, describe them with sketches, words, or input/output tables.
Note that this table was in no way “rigged.” For any finite table, even if it had thousands of entries, there are an infinite number of functions that fit it. Usually, there will be one “simplest” function. But sometimes it’s not clear what’s simple: Is a quadratic function “simpler” than an exponential function? Is a linear function “simpler” than a cyclic function?
Solutions
Problem C1
Here is the completed table:
Problem C2
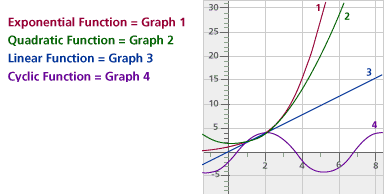
Problem C3
An infinite number of functions share these two data points. There are too many rules that turn the input of 1 into the output of 2 and the input of 2 into the output of 4. The rule could be as complicated as Mr. Lewis’s rule from Session 2, or it could be as simple as the house numbers on the left side of your street.
Some examples: y = 3x-1 + 1; y = n (n + 1) / 2 + 1; y = the date number, every other day, starting with January 2.
