Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
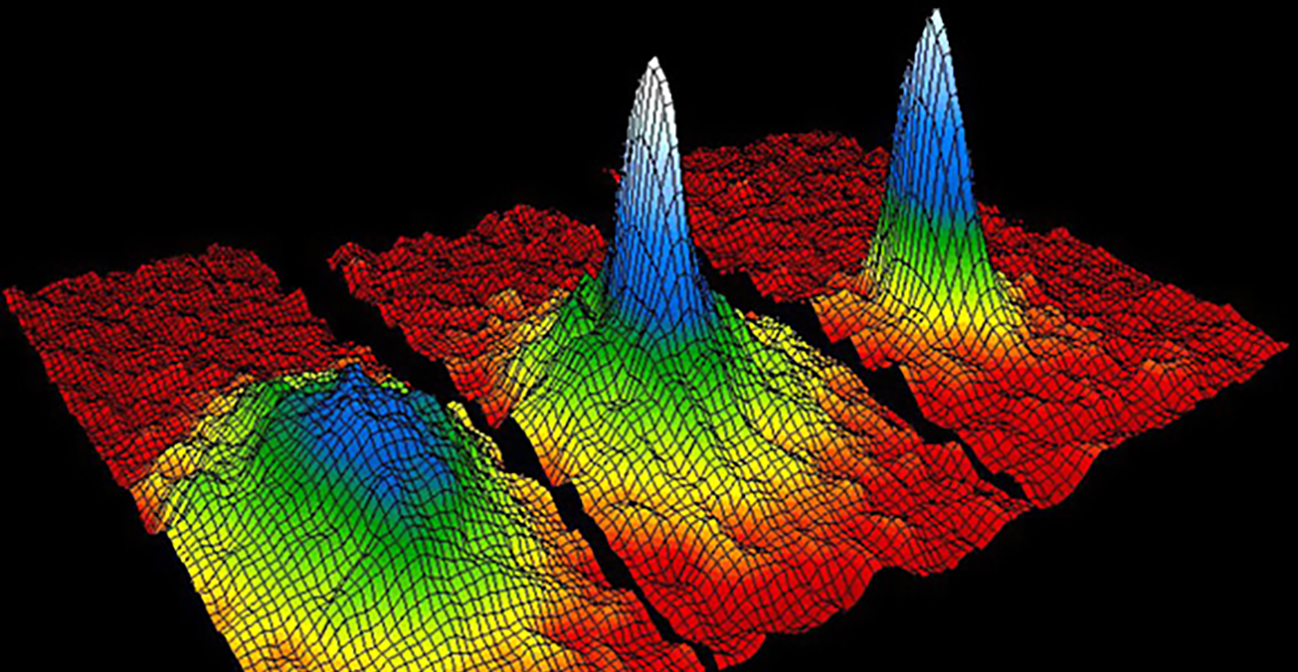
The fundamentals of quantum mechanics that we met in Unit 5 characteristically appear on microscopic scales. Macroscopic quantum systems in which liquids, or electric currents, flow without friction or resistance have been known since the early part of the previous century: these are the superfluids and superconductors of traditional condensed matter physics that are discussed in Unit 8. In this unit we focus on an entirely new state of matter only recently created in the laboratory: this is the gaseous macroscopic quantum mechanical system known as a Bose-Einstein Condensate, or BEC. These quantum gases show the full panoply of quantum wave behavior as the individual particles of Unit 5, but now on a size scale visible to the naked eye because many millions, to many billions, of atoms occupy exactly the same quantum state, and thus form a coherent quantum whole. The quantum nature of a BEC can be directly visualized as the quantum effects are not hidden within liquids or solids as is the case with the more traditional superfluids and superconductors. Rather, they may be actually photographed, as the gas itself is a naked macroscopic quantum system. This unit starts by introducing the basic principles necessary to understand BECs, then details how the cooling and trapping introduced in Unit 5 led to the creation and subsequent manipulation of these quantum gases. Finally, we will see how atomic gases of ultra-cold fermions have evolved, in direct analogy to the Cooper paring needed to form bosonic pairs of electrons in superconductors, to molecular BECs, formed from pairs of the fermionic atoms.
alkali metals
The alkali metals are the chemical elements in the first column of the periodic table. They all have one valence electron. Alkali metals are commonly used atoms in atomic physics experiments for several reasons. Their structure is relatively simple and provides energy states that are convenient for laser cooling. Many of their transition frequencies match convenient laser sources. Also, the single valence electron’s magnetic moment allows the atoms to be easily trapped using magnetic fields, which is convenient for the evaporative cooling process necessary to reach ultracold temperatures.
atomic number
The atomic number of an atom, denoted by Z, is the number of protons in its nucleus. The atomic number of an atom determines its place in the periodic table, and thus which chemical element it is.
blackbody
A blackbody is an object that absorbs all incident electromagnetic radiation and re-radiates it after reaching thermal equilibrium. The spectrum of light emitted by a blackbody is smooth and continuous, and depends on the blackbody’s temperature. The peak of the spectrum is higher and at a shorter wavelength as the temperature increases.
Bose-Einstein condensate
A Bose-Einstein condensate, or BEC, is a special phase of matter in which the quantum mechanical wavefunctions of a collection of particles line up and overlap in a manner that allows the particles to act as a single quantum object. The electrons in a superconductor form a BEC; superfluid helium is an example of a liquid BEC. BECs can also be created from dilute gases of ultracold atoms and molecules.
boson
A boson is a particle with integer, rather than half-integer, spin. In the Standard Model, the force-carrying particles such as photons are bosons. Composite particles can also be bosons. Mesons such as pions are bosons, as are 4He atoms. See: fermion, meson, spin.
complex
In the context of physics and math, the term complex refers to the presence of complex numbers and is not a synonym of complicated. Thus, a “complex wave” is a mathematical function that describes a wave that can take on complex number values.
complex number
A complex number is a composite of a real number and an imaginary number, and can be written in the form a+bi where a and b are real numbers and i is the square root of -1.
counting number
The counting numbers are the integers greater than zero: 1, 2, 3 … .
de Broglie wavelength
A particle’s de Broglie wavelength, , is defined as Planck’s constant divided by the particle’s momentum, p:
= h/p. The de Broglie wavelength is named after Louis de Broglie, the French physicist who first suggested that it might be useful to describe particles as waves. A relativistic electron has a de Broglie wavelength of around a nanometer, while a car driving down the highway has a de Broglie wavelength of around 10-38 meters. Quantum mechanical effects tend to be important at the scale of an object’s de Broglie wavelength; thus we need to describe electrons quantum mechanically, but classical physics is adequate for cars and most other macroscopic objects.
electric dipole moment
The electric dipole moment of a system with two electric charges is defined as the product of the two charges divided by the distance between them. It is a vector quantity, with the positive direction defined as pointing from the (more) negative charge toward the (more) positive charge. The electric dipole moment of a more complicated system of charges is simply the sum of the moments of each pair of charges.
fermion
A fermion is a particle with half-integer spin. The quarks and leptons of the Standard Model are fermions with a spin of 1/2. Composite particles can also be fermions. Baryons, such as protons and neutrons, and atoms of the alkali metals are all fermions. See: alkali metal, baryon, boson, lepton, spin.
ground state
The ground state of a physical system is the lowest energy state it can occupy. For example, a hydrogen atom is in its ground state when its electron occupies the lowest available energy level.
harmonic trap
A harmonic trap is a trap in which the trapped objects (e.g., atoms) are pushed toward the center of the trap with a force proportional to their distance from the center of the trap. The motion of particles in a harmonic trap is analogous to the motion of a mass attached to a spring around the spring’s equilibrium position. It is convenient to use harmonic traps in experiments because it is straightforward to calculate the motion of particles in analogy to the mass on a spring.
hyperfine structure
When the nucleus of an atom has a nonzero magnetic moment, some of the energy levels that electrons can occupy in the atom are very finely spaced. The arrangement of these finely spaced levels is called “hyperfine structure.” The difference in energy between hyperfine levels typically corresponds to a microwave photon frequency or light with a wavelength on the order of centimeters. The energy levels in the cesium atom used to define the second are hyperfine levels.
imaginary number
An imaginary number is a real number multiplied by the square root of -1, which is denoted by i.
ion
An ion is an atom with nonzero electrical charge. A neutral atom becomes an ion when one or more electrons are removed, or if one or more extra electrons become bound to the atom’s nucleus.
isotope
Different atoms of a chemical element in the periodic table all have the same number of protons, but may have a different number of neutrons in their nuclei. These different versions of the same element are called isotopes. The number of neutrons is not simply random, however—the nucleus will only be stable for combinations of protons and neutrons. Most chemical elements have several stable isotopes. For example, lithium (A=3) has two stable isotopes, one with three neutrons in the nucleus (6Li) and one with four (7Li). See: atomic number, mass number.
macroscopic
A macroscopic object, as opposed to a microscopic one, is large enough to be seen with the unaided eye. Often (but not always), classical physics is adequate to describe macroscopic objects, and a quantum mechanical description is unnecessary.
magnetic moment
The magnetic moment (or magnetic dipole moment) of an object is a measure of the object’s tendency to align with a magnetic field. It is a vector quantity, with the positive direction defined by the way the object responds to a magnetic field: The object will tend to align itself so that its magnetic moment vector is parallel to the magnetic field lines. There are two sources for a magnetic moment: the motion of electric charge and spin angular momentum. For example, a loop of wire with a current running through it will have a magnetic moment proportional to the current and area of the loop, pointing in the direction of your right thumb if your fingers are curling in the direction of the current. Alternatively, an electron, which is a spin-1/2 fermion, has an intrinsic magnetic moment proportional to its spin.
mass number
The mass number (or atomic mass number) of an atom, denoted by A, is the total number of nucleons (protons+neutrons) in its nucleus. Sometimes, the mass number of an atom is written as a superscript to the left of its chemical symbol (e.g., 6Li) to show which isotope is being discussed. See: atomic number, isotope.
node
Nodes are the positions in a standing wave that do not move as the wave oscillates. Antinodes are the opposite of nodes—the positions in a standing wave that move up and down the most as the wave oscillates. A plucked guitar string oscillating in its fundamental mode has a node at each end, and an antinode in the middle.
Pauli exclusion principle
The Pauli exclusion principle states that no two identical fermions can occupy the same quantum state. It plays an important role in determining the structure of atoms and atomic nuclei, as well as how electrons behave in metals and semiconductors.
phase
In physics, the term phase has two distinct meanings. The first is a property of waves. If we think of a wave as having peaks and valleys with a zero-crossing between them, the phase of the wave is defined as the distance between the first zero-crossing and the point in space defined as the origin. Two waves with the same frequency are “in phase” if they have the same phase and therefore line up everywhere. Waves with the same frequency but different phases are “out of phase.” The term phase also refers to states of matter. For example, water can exist in liquid, solid, and gas phases. In each phase, the water molecules interact differently, and the aggregate of many molecules has distinct physical properties. Condensed matter systems can have interesting and exotic phases, such as superfluid, superconducting, and quantum critical phases. Quantum fields such as the Higgs field can also exist in different phases.
phase coherence
If we think of a wave as having peaks and valleys with a zero-crossing between them, the phase of the wave is defined as the distance between the first zero-crossing and the point in space defined as the origin. Two waves are phase coherent (or simply coherent) if the distance between their respective peaks, valleys, and zero-crossings is the same everywhere.
photon
Photons can be thought of as particle-like carriers of electromagnetic energy, or as particles of light. In the Standard Model, the photon is the force-carrier of the electromagnetic force. Photons are massless bosons with integer spin, and travel through free space at the speed of light. Like material particles, photons possess energy and momentum.
Planck’s constant
Planck’s constant, denoted by the symbol h, has the value 6.626 x 10-34 m2 kg/s. It sets the characteristic scale of quantum mechanics. For example, energy is quantized in units of h multiplied by a particle’s characteristic frequency, and spin is quantized in units of h/2. The quantity h/2
appears so frequently in quantum mechanics that it has its own symbol:
.
plum pudding model
The Plum Pudding Model is a model of atomic structure proposed by J.J. Thomson in the late 19th century. Thomson had discovered that atoms are composite objects, made of pieces with positive and negative charge, and that the negatively charged electrons within the atom were very small compared to the entire atom. He therefore proposed that atoms have structure similar to a plum pudding, with tiny, negatively charged electrons embedded in a positively charged substrate. This was later shown to be incorrect.
polar
A polar molecule has a nonzero electric dipole moment, so it has a side that is positively charged and a side that is negatively charged.
probability density
The exact location of a quantum mechanical particle is impossible to know because of the Heisenberg uncertainty principle. Rather than specifying the location of a particle such as an electron, quantum mechanics specifies a wavefunction. The probability density, which is a mathematical function that specifies the probability of finding the particle at any location in space, is the square of the wavefunction (technically, its absolute value squared).
real number
Real numbers are most easily defined by contrast to what they are not: imaginary numbers. The set of real numbers includes counting numbers, integers, rational numbers that can be written as fractions, and irrational numbers such as . They can be thought of as all the points on a number line stretching from negative infinity to infinity.
shell model
The shell model of atomic structure is based on the notion that electrons in an atom occupy “shells” that can fill up, so only a certain number of electrons will fit in a given shell. G. N. Lewis found this idea useful in explaining the chemical properties of different elements. Lewis’s shell model is consistent with the Bohr model of the atom in which electrons are thought of as orbiting the nucleus. The “shells” are three-dimensional counterparts of two-dimensional circular orbits with different radii. Although we now know that the Bohr model of the atom is not correct, the concept of shells is still sometimes used to describe the arrangement of electrons in atoms according to the Pauli exclusion principle.
soliton
A soliton is a stable, isolated wave that travels at a constant speed. As a soliton travels, its shape does not change and it does not dissipate. If it collides with another wave, it emerges from the collision unscathed. In a sense, it is a wave that behaves like a particle. Solitons have been predicted and observed in nearly every medium in which waves propagate, including fluids such as water, transparent solids such as optical fibers, and magnets.
standing wave
A standing wave is a wave that does not travel or propagate: The troughs and crests of the wave are always in the same place. A familiar example of a standing wave is the motion of a plucked guitar string.
valence electron
A valence electron is an electron in the outermost shell of an atom in the Lewis model, or in the orbital with the highest value of the principal quantum number, n, in the quantum mechanical description of an atom. The valence electrons determine most of the chemical and physical properties of the atom. It is the valence electrons that participate in ionic and covalent chemical bonds, and that make the primary contributions to an atom’s magnetic moment.
vortex
A vortex is a region in which a fluid or gas flows in a spiral toward the vortex center. The speed of fluid flow is fastest at the center of the vortex, and decreases with distance from the vortex center. Tornados and whirlpools are examples of vortices. Quantized vortices will appear in a superfluid when it is rotated fast enough, and quantized vortices will form in the electron gas inside a type-II superconductor when it is placed in a strong enough magnetic field.

William P. Reinhardt is a professor of chemistry and adjunct professor of physics at the University of Washington. His research is in two main areas: (1) modeling the structure and dynamics of the newest state of matter, the gaseous Bose-Einstein condensate (BEC); and, (2) development of novel techniques for determination of the entropies and free energies of complex molecular systems, including clusters and polymers. This work, leading to the present contribution, has been long supported by National Science Foundation (NSF) Chemistry and/or NSF Physics; this is most gratefully acknowledged.

Jenny Hoffman is an assistant professor of physics at Harvard University. Her research uses several scanning probe microscopes to study novel materials in which electrons interact strongly, leading to exotic behaviors such as high temperature superconductivity. One focus of her research is imaging magnetic vortices in superconductors, both to understand their technological impact, and as nanoscale windows into unexplored regions of phase space in these materials. Prior to coming to Harvard, she earned her Ph.D. in 2003 from the University of California at Berkeley, then worked as a postdoctoral fellow in Stanford’s applied physics department.

Deborah S. Jin is a physicist with the National Institute of Standards and Technology (NIST), Professor Adjoint, Department of Physics at the University of Colorado, and a fellow of the Joint Institute for Laboratory Physics (JILA), a NIST joint laboratory with the University of Colorado. She won the prestigious MacArthur Fellowship “genius grant” in 2003, and in 2004 she was recognized by Scientific American as “Research Leader of the Year.” In 2008 she received the Benjamin Franklin Medal in Physics for her pioneering investigations of the quantum properties of an ultracold gas of fermionic atoms, atoms that cannot occupy the same quantum state, and in particular for the creation of the first quantized gas of fermionic atoms.