In the mx

Objective:
Child will use similar triangles to determine slope and interpret unit rates as slopes.

Essential Question:
How might we use triangles to determine the rate of change?

Special Materials:
None

Bricks Required:
1x bricks of various sizes; two brick plates

Project Structure

Engage/Explain:

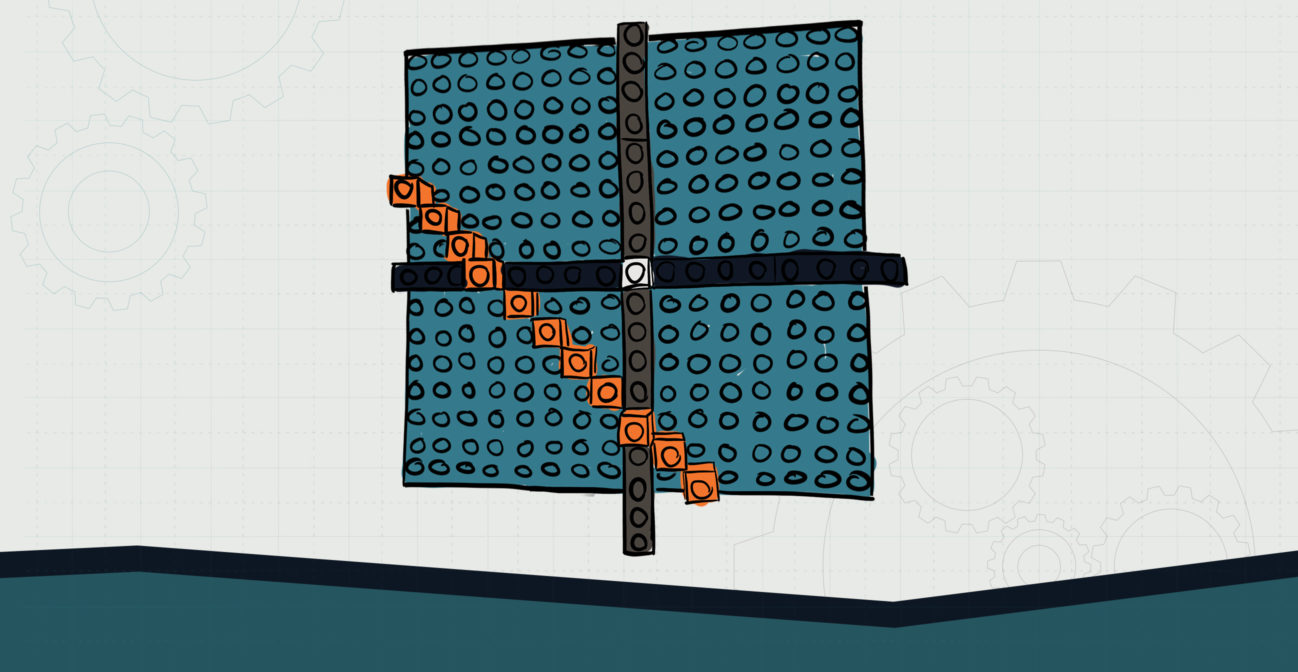
1. Provide child with an equation of a line that they can easily graph using SOHO Bricks. For example, y = (2/1) x + 1. Child should graph by plugging in values for x and determining the y coordinate.
2. Ask child to reflect upon the equation and the graph.
   1. “Looking at your graph, where does the line cross the y axis?”
   2. “Looking at your equation, how might you be able to tell where it crossed the y axis?”
   3. “Do you think the equation will always tell you where the line will cross the y axis? Why or why not?”
   4. “Does the equation tell us anything else about the graph?”
      1. Facilitate child to think about the “mx” portion of the equation. How is it represented in the graph?
      2. Through observation and exploration, child may discover that each point increases in the y direction by 2 units while the x increases by 1 unit, and that this is the visible component in front of the x.

Explore:

1. Ask child to provide an explanation of how they know that the x and y coordinates move 2/1 every time.
2. Ask child to prove that this works if they do not count from one point to another. In other words, can they skip points and still get the same results?
   1. Child may elect to use bricks to construct triangles from any two points;
   2. Child may not see at first that their results are the same.
3. Work with child to demonstrate that similar triangles will always result in the same ratio of 2/1 for this line. This is called the slope or the rate of change.
4. See if child can construct an equation to determine the slope.
5. Discuss the slope formula.
   1. How does this fit our understanding of rate of change and our similar triangles?

Explain/Elaborate:

1. Provide child additional problems to determine the rate of change for each problem and they intercept.
2. Child may do these on graph paper and sketch triangles to show the ratio of the rate of change (slope).

Further Elaboration (The SOHO Stack):

1. In this activity, child will have an opportunity to blend science and math by performing a SOHO Brick stack.
2. Take turns with your child stacking as many bricks as they as you can in a given time allotment: 1 second, 2 seconds, 3 seconds, etc. Each attempt should be repeated at least 3 times and the average taken.
3. Child then plots their own data, determines the line of best fit, finds the slope of their line using similar triangles, and determines which had the fastest rate of brick-stacking.