Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
The word “trigonometry” is enough to strike fear into the hearts of many high school students. But it simply means “triangle measuring.” A trigon is another name for a triangle — think pentagon and hexagon, for example — and “-metry” means “measuring,” just as it does in “geometry,” or “earth measuring.” Trigonometry is about measuring similar right triangles.
 Set up a proportion between the corresponding sides of the two triangles, the original one and the new one with unknown sides. There are many different proportions you might set up depending on what you’re looking for (e.g., a1/c1 = a2/c2, or, a1/a2 = c1/c2, etc.). In each proportion try to use three known side lengths, so the only unknown is the side you’re looking for.
Set up a proportion between the corresponding sides of the two triangles, the original one and the new one with unknown sides. There are many different proportions you might set up depending on what you’re looking for (e.g., a1/c1 = a2/c2, or, a1/a2 = c1/c2, etc.). In each proportion try to use three known side lengths, so the only unknown is the side you’re looking for.
Here’s a right triangle:

The triangles below are all similar to the original triangle above. Find the length a for each triangle. Explain how you did it. Note 7

For each triangle above, find the length b. Explain how you did it.
If you solved the problems above, you probably used the sine and cosine functions, even if you didn’t know you were doing it. To find the missing value of a, you need to multiply the length of the hypotenuse by 3/5. To find the length b, you multiply the hypotenuse by 4/5.
Those ratios — (side a)/(hypotenuse) = 3/5 and (side b)/(hypotenuse) = 4/5 — will hold for any right triangle that has another angle the same as A. All such right triangles will be similar to each other, so the ratios must be the same as in our original triangle.
As you’ve seen, the trigonometric functions such as sine, cosine, and tangent are nothing more than ratios of particular sides in right-angle triangles. Note 8 These ratios depend only on the measure of an angle and have special names:


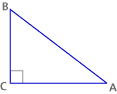

In the triangle above, the sine of angle A is defined as BC/AB. It is abbreviated sin A.
The cosine of angle A is defined as AC/AB. It is abbreviated cos A.
The tangent of angle A is defined as BC/AC. It is abbreviated as tan A. Note 9
Use the Interactive Activity to answer Problem C3 and C4 and to experiment with the trigonometric functions. For example, how big can sine get? What about cosine? How do you make them as big as possible? What about tangent? Does it seem to have a maximum value? (This interactive has been disabled due to Flash content.)
For the original triangle:

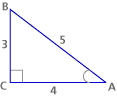
| a. | Find sin A and cos A. |
| b. | Find sin B and cos B. |
For the following triangle:

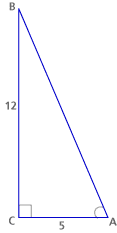
| a. | Find sin A and cos A. |
| b. | Find sin B and cos B. |
| c. | Find tan A and tan B. |
| a. | Find sin 30°, cos 30°, and tan 30° in the triangle below. Then find sin 60°, cos 60°, and tan 60°. |
| b. | Find sin 45°, cos 45°, and tan 45° in the triangle below.
|
Suppose you have any right triangle ABC (with the right angle at C). Explain why it must be true that sin A = cos B.
Most public buildings were built before wheelchair-access ramps became widespread. When it came time to design the ramps, the doors of buildings were already in place. Suppose a particular building has a door two feet off the ground. How long must a ramp be to reach the door if the ramp is to make a 10° angle with the ground? (This is why so many access ramps must make one or more turns!)

sin 10° ![]() 0.17 and cos 10°
0.17 and cos 10° ![]() 0.98 Note 10
0.98 Note 10
Problem C7 taken from Connected Geometry, developed by Educational Development Center, Inc. p. 341. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
If you’re working with a group, compare different methods other participants have come up with. Think about how these methods connect to yours.
These ratios have been immensely useful in many fields, such as engineering, surveying, astronomy, and architecture. In addition to the three trigonometric functions mentioned in this session (sine, cosine, and tangent), there are three additional functions not covered in this course (secant, cosecant, and cotangent).
In mathematics, if we have an idea that works in some particular cases, we often look for ways to extend that idea to a more general situation. For example, the definitions of the trigonometric functions on the right triangle are valid only when dealing with angles between 0° and 90° — no other angle can appear in a right triangle!
So, in order to make sense of and compute the values of trigonometric functions of any angle, we need to extend this definition. According to the extended definition, sin and cos of angle ![]() (theta) are defined to be y and x coordinates, respectively, of a point on the unit circle. (The unit circle is a circle centered at the origin of the coordinate system, with a radius equal to 1.)
(theta) are defined to be y and x coordinates, respectively, of a point on the unit circle. (The unit circle is a circle centered at the origin of the coordinate system, with a radius equal to 1.)

Notice that as we move the point P along the circle to create angles between 0° and 360°, some coordinates will be positive and some will be negative.
The values for sine and cosine have been calculated for many triangles. You can find them in a trigonometry table, or you can calculate them yourself using a scientific calculator.
The triangle with hypotenuse 4: By similarity with the original triangle, we can say:
5/4 = 3/a, so a = 12/5.
The triangle with hypotenuse 10: By similarity with the original triangle, we can say:
5/10 = 3/a, so a = 30/5 = 6.
The triangle with hypotenuse 1: By similarity with the original triangle, we can say:
5/1 = 3/a, so a = 3/5.
The triangle with hypotenuse 4: By similarity with the original triangle, we can say:
5/4 = 4/b, so b = 16/5.
The triangle with hypotenuse 10: By similarity with the original triangle, we can say:
5/10 = 4/b, so b = 40/5 = 8.
The triangle with hypotenuse 1: By similarity with the original triangle, we can say:
5/1 = 4/b, so b = 4/5.
a. sin A = 3/5 and cos A = 4/5
b. sin B = 4/5 and cos B = 3/5
Problem C4
We calculate the hypotenuse with the Pythagorean theorem and find that it is 13.
| a. | sin A = 12/13, cos A = 5/13 |
| b. | sin B = 5/13, cos B = 12/13 |
| c. | tan A = 12/5, tan B = 5/12 |
Problem C5
| a. | sin 30° = cos 60° = 1/2 sin 60° = cos 30° = √3/2 tan 30° = 1/√3 tan 60° = |
| b. | sin 45° = cos 45° = 1/√2 tan 45° = 1These values are constant for any triangle with angles 45°-45°-90°. |
Angles A and B are adjacent, so sin A = cos B. The hypotenuse is the same for both angles, but the roles of “adjacent side” and “opposite side” switch. The side opposite angle B is adjacent to angle A, and vice versa.
Let x be the length of the ramp. Then we have a right triangle with hypotenuse x, shorter leg 2, and the angle opposite to the shorter leg of 10°. Since sin 10° = 2/x, we have x = 2/sin 10° = 2/0.17 ![]()
 11.765 feet.
11.765 feet.