Private: Learning Math: Geometry

Professional Development > Private: Learning Math: Geometry > 4. Parallel Lines and Circles > 4.2 Part B: Parallel Lines (45 minutes)

Mathematics

K-2, 3-5, 6-8

Parallel Lines and Circles Part B: Parallel Lines (45 minutes)

Session 4, Part B

In this part:

Properties of Angles
Reasoning About Properties of Angles

Properties of Angles

Parallel lines are two lines in the same plane that never intersect. Another way to think about parallel lines is that they are “everywhere equidistant.” No matter where you measure, the perpendicular distance between two parallel lines is constant. With dynamic geometry software, you can draw two lines that look parallel, but you can’t be sure that they are parallel unless you construct them to be parallel. Note 2

Problem B1

Follow these steps to construct two parallel lines:

a.	Using the Line Tool in Geometer’s Sketchpad, draw a line.
b.	Pull down the Construct menu in Sketchpad. You’ll notice that the “Parallel Line” is gray — therefore, not an option to you. This is Sketchpad’s way of telling you that you don’t have the correct objects selected or you don’t have enough objects selected. What else do you need to construct a line parallel to your original line?
c.	Continue your construction and record the steps you used to construct two parallel lines.

Problem B2

To measure an angle, select three points in the order of the angle. You may need to construct additional points on your lines before you can measure the angles.

Draw a transversal through your parallel lines. (A transversal is a line that passes through two parallel lines.)

a.	Measure each of the angles formed.
b.	Change the orientation of the transversal by dragging one of the defining points. Keep a record of what changes and what stays the same.

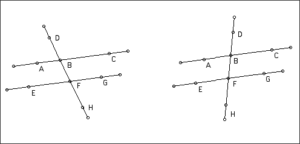
When a pair of parallel lines is cut by a transversal, several special pairs of angles are formed.

∠ABD and ∠EFB are corresponding angles.
∠ABF and ∠GFB are alternate interior angles.
∠ABD and ∠CBF are vertical angles.
∠ABD and ∠CBD form a linear pair.

Problem B3

Name another pair of corresponding angles, another pair of alternate interior angles, another pair of vertical angles, and another linear pair.

Problem B4

Using this new terminology, summarize the relationships you discovered in Problem B2.

Reasoning About Properties of Angles

In the previous subpart, you gathered evidence of some properties of angles. But evidence alone doesn’t explain why something is true, or even mean that it is true. Mathematics requires a reasoned argument that is general, not about a specific set of lines.

When two lines intersect, the vertical angles (angles opposite each other) have the same measure.

Problem B5

In this problem, you will look at an explanation for why vertical angles have the same measure.

a.	m∠1 + m∠2 = 180°. Why?
b.	Also m∠3 + m∠2 = 180°. Why?
c.	So m∠1 must equal m∠3. Why?
d.	What other pair of angles is equal in measure? Why?

When two parallel lines both intersect a third line, corresponding angles (angles in the same relative positions, like angles 1 and 7 or angles 3 and 5 in the picture below) have the same measure.

One way to understand this is to imagine sliding a copy of the picture above along line j until line k sits on top of line l. (Note 3)

Now ∠1 sits exactly where ∠7 used to be, ∠3 sits exactly where ∠5 used to be, and so on.

To prove that corresponding angles are congruent, we could add another line segment, , parallel to line j. By doing so we have created a parallelogram, and thus we know that the adjacent angles of a parallelogram (in this case ∠2 and ∠7) equal 180°.

So, to prove that ∠1 and∠7 are congruent, we write the following:

∠1 +∠2 = 180° (because they form a straight line)
∠2 +∠7 = 180° (because they are adjacent angles of a parallelogram)

It follows that∠1 +∠2 = ∠2 +∠7 = 180°.

And thus, ∠1 =∠7

Alternate interior angles (angles on opposite sides of the transversal, and between the parallel lines, like∠7 and∠3 or∠2 and∠8), also have the same measure.

Problem B6

Create an argument to explain why the above statement about alternate interior angles would be true. You may want to use the facts about corresponding angles and vertical angles, or you may come up with another explanation.

Problem B7

Create any quadrilateral with Geometer’s Sketchpad. Construct the midpoints of all four sides of the quadrilateral, and then connect them in order.

a.	Describe the quadrilateral in the center.
b.	How could you test to see if you are right about the kind of quadrilateral you have in the center? What measurements could you make?
c.	Move around your original quadrilateral, changing its shape. What changes on the inside quadrilateral? What stays the same?
d.	How can you change your original quadrilateral to make the inside quadrilateral a square?

Notes

Note 2

Discuss or reflect on why “in the same plane” is an important part of the definition. If you think in three dimensions, two lines can never intersect but also be not parallel. To demonstrate this, you can draw a line on one piece of paper, then draw a line on another piece of paper. Put one of the pieces of paper on a table or desk, and hold the second one above the first, parallel to it. You can rotate the second piece of paper and see that the two lines will never intersect as long as the planes (papers) stay parallel, but the lines are not always parallel to each other.

Note 3

If you are working in a group, you can also demonstrate this for the whole group with an overhead projector. Make two copies of the j, k, l setup on transparencies. Place both transparencies on the overhead projector, one on top of the other. Then slide the top transparency, keeping one line j on top of the other. Lines k and l very convincingly match up.