Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Geometry
The Pythagorean Theorem Part A: The Pythagorean Theorem (20 minutes)
Session 6, Part A
In this part
- Calculating Area
- Squares Around a Right Triangle
- The Theorem
Calculation Area
Here is a square drawn on dot paper:
Problem A1
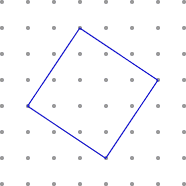
Come up with a method to find the exact area of the square in square units. You can either use calculations or count the square units.
Problem A1 adapted from IMPACT Mathematics, Course 1, developed by Educational Development Center, Inc. p. 536. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
Squares Around a Right Triangle
Problem A2
Each of the three figures in Problem A2 shows a right triangle with squares built on the sides. Determine the exact area of all three squares for each figure.
Figure 1:  |
Figure 2: |
Figure 3:  |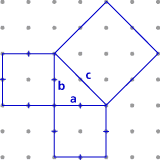
|
Figure # |
Area of Square on Side a |
Area of Square on Side b |
Area of Square on Side c |
| Figure 1: | |||
| Figure 2: | |||
| Figure 3: |
Problem A3
Look at your table, and come up with a relationship between the three squares that holds for all of the pictures.
|
|
Video SegmentIn this video segment, the participants calculate the areas of the squares built on the right triangles. As they do the activity, a pattern begins to emerge, and they are able to formulate the relationship they discovered. Was your method of calculating areas similar to or different from the one shown here? Can you come up with yet another way of doing this? You can find this segment on the session video approximately 4 minutes and 58 seconds after the Annenberg Media logo. |
Problem A2 and the Video Segment problems adapted from IMPACT Mathematics, Course 1, developed by Educational Development Center, Inc. p. 537. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
The Theorem
In a right triangle, the side opposite the right angle (side c in all of the pictures in Problem A2) is called the hypotenuse.
The problems you just solved illustrate the Pythagorean theorem: In a right triangle, the square built on the hypotenuse is equal in area to the sum of the squares built on the other two sides.
Today, most people think of the theorem as stating a relationship among three numbers, a, b, and c, which represent the lengths of the sides of a right triangle.
The Pythagorean theorem is named for Pythagoras, a Greek mathematician who lived from about 569-500 B.C.E., around the same time as Lao-Tse, Buddha, and Confucius. Pythagoras was the leader of a society that would likely be considered a cult by modern standards. They studied mathematics and numerology, were very superstitious about what they ate and how they lived, and were sworn to secrecy.
Part A: The Theorem adapted from Connected Geometry, developed by Educational Development Center, Inc. p. 197. © 2000 Glencoe/McGraw Hill. Used with permission. www.glencoe.com/sec/math
Solutions
Problem A1
Draw a square with side lengths of 5 units around the given square so that the vertices of the given square are on the sides of the new square. The area of the new square is 25 square units (since its side length is 5), and its area is larger than the area of the original square by the area of the four right triangles whose legs have lengths of 2 and 3 units. So the area of the original square is 25 – 4 • (3 • 2 / 2) = 13 square units.
| It looks like this:
|
 |
Another method is the following:
Again, the area of the square is 4 • (2 • 3 / 2) + 1 • 1 = 13 square units. |
Problem A2
Using the same method from A1, here are the areas:
|
Figure # |
Area of Square on Side a |
Area of Square on Side b |
Area of Square on Side c |
| Figure 1: | 4 | 9 | 13 |
| Figure 2: | 1 | 4 | 5 |
| Figure 3: | 4 | 4 | 8 |
Problem A3
The area of the square on side c is always the sum of the areas of the squares on the other two sides.
