Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
The Pythagorean theorem is useful for finding missing lengths. If you can find a right triangle in a picture, you can often find the length you need. All you need to know is that if a2 + b2 = c2, then ![]() That is, you can take the square root of both sides of the equation. Because you’re working with lengths (so all the values are positive), you can find c.
That is, you can take the square root of both sides of the equation. Because you’re working with lengths (so all the values are positive), you can find c.
Draw a picture and look for right triangles.
Find the length of the diagonal of a square whose sides have the following lengths:
| a. | 1 foot |
| b. | 2 feet |
| c. | 10 feet |
| d. | n feet |
Find the lengths of all the segments that are not labeled in the picture below. Describe a pattern in the lengths.

The perpendicular bisector of a segment is perpendicular to the segment and goes through the midpoint. Show that any point on the perpendicular bisector of a segment is the same distance from each of the endpoints.
The line is the perpendicular bisector of AB. Use the Pythagorean theorem to explain why PA and PB (the dashed segments) are the same length.

Problems C1-C3 adapted from Connected Geometry, developed by Educational Development Center, Inc. pp. 65, 205, 206. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
“As long as algebra and geometry have been separated, their progress has been slow and their uses limited; but when these two sciences have been united, they have lent each mutual forces, and have marched together towards perfection.”
— Joseph-Louis Lagrange (1736-1813)
French mathematician René Descartes (1596-1650) was the first to employ algebra in solving geometry problems. His key insight, and one that has affected the study of mathematics ever since, was that of the development of coordinate geometry (or Cartesian geometry, named for its creator).

By convention, the axes are shown in the horizontal and vertical positions. The horizontal axis is called the x-axis, and the vertical is called the y-axis. When you describe a point, you list the coordinates in order (x,y). There’s nothing magical in these conventions; they just make it easy for everyone to understand each other.
The coordinates of the point are about (2.1,1.4).
To use the power of algebra to solve problems in geometry, you need the distance formula — a way to measure the distance between two points. Luckily, the distance formula is just a special case of the Pythagorean theorem, so you don’t have to remember anything new.
Find the distances between the following:
| a. | A = (0,0) and B = (1,1) |
| b. | A= (2,3) and B = (-1,-1) |
| c. | A = (-3,-2) and B = (5,4) |
| d. | A = (-3,4) and B |
| e. | A= (-2,-3) and B |
| f. | A = (-3,-1) and B |
![]() Try constructing a right triangle whose hypotenuse is a line segment connecting points A and B, with a as its horizontal side (parallel to the x-axis). Then use the distance formula, the algebraic version of the Pythagorean theorem.
Try constructing a right triangle whose hypotenuse is a line segment connecting points A and B, with a as its horizontal side (parallel to the x-axis). Then use the distance formula, the algebraic version of the Pythagorean theorem.
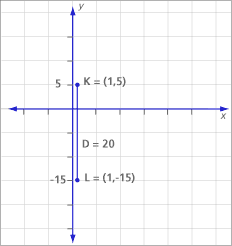
Plot the given pair of points and find the distance between them.
| a. | I = (10,-7) and J = (2,-7) |
| b. | K = (1,5) and L = (1,-15) |
| c. | A = (x,a) and B = (x,b) |
| d. | A = (a,y) and B = (b,y) |
 In parts (c) and (d), make sure your answer takes into consideration that you don’t know whether length a or b is greater. Is there a way to be sure your answer is never negative?
In parts (c) and (d), make sure your answer takes into consideration that you don’t know whether length a or b is greater. Is there a way to be sure your answer is never negative?
Find the distance between the two points pictured: A=(x1,y1) and B=(x2,y2).

Diagram in Part C: Distance Formula adapted from Connected Geometry, developed by Educational Development Center, Inc. p. 355. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
 In all four parts of the problem, we draw a diagonal of length d inside the square of side length a, dividing the square into two congruent right triangles (see picture). Using the Pythagorean theorem, we get a2 + a2 = d2, or
In all four parts of the problem, we draw a diagonal of length d inside the square of side length a, dividing the square into two congruent right triangles (see picture). Using the Pythagorean theorem, we get a2 + a2 = d2, or ![]() .
.
So we get the following:
a. √2 feet
b. 2√2 feet
c. 10√2 feet
d. n√2 feet
All the segments are right triangles, so we can apply the Pythagorean theorem. The smallest one has both legs of length 1, so its hypotenuse has length√2 (as in part (a) of Problem C1). The next smallest triangle has legs of length 1 and√2, so its hypotenuse has length![]() . Similarly, the length of the hypotenuse of the next smallest triangle is √4=2. Following the pattern, the length of the hypotenuse of the nth triangle is √n+1, so the last hypotenuse has length √14.
. Similarly, the length of the hypotenuse of the next smallest triangle is √4=2. Following the pattern, the length of the hypotenuse of the nth triangle is √n+1, so the last hypotenuse has length √14.
Let O be the point of intersection of the line segment AB and its perpendicular bisector. The lengths AO and OB are congruent since O bisects AB. The angles AOP and POB are both right angles since the bisector is perpendicular. So, by using the Pythagorean theorem, we get
AP2 = AO2 + OP2
![]()
By a similar argument we can say that
![]()
We know, however, that AO and BO are the same length, since O is the midpoint of segment AB. This means that the two values under the square root are the same, and AP must be the same length as BP.

This can also be proven with SAS triangle congruence, which you first saw in the Session 2 Homework. It states that if two triangles have two sides equal in length and the angles between those sides are equal in their degree measure, then the two triangles are congruent. We know that the lengths AO and OB are congruent since O bisects AB. We also know that they share side OP. The angle between those two sides in each triangle is 90° since the bisector is perpendicular to AB. Thus, the two triangles are congruent, and so AP and BP are the same length.
a. The distance we want is the length of the line segment AB, which happens to be a hypotenuse of an isosceles right triangle whose legs have a length of 1 unit. Using the Pythagorean theorem, the distance we get is √12+12=√2.

b. From the point A = (2,3), draw a line perpendicular to the x-axis. Similarly, from B = (-1,-1), draw a line perpendicular to the y-axis. We will call the point where the two lines intersect point C. Then ABC is a right triangle whose hypotenuse AB is the distance between A and B. Using the Pythagorean theorem, we can calculate the distance as follows:
D=√42+32 = √25 = 5

c. Using the Pythagorean theorem, we can calculate the distance as follows:
D=√82+62 = √100 = 10

d. Using the Pythagorean theorem, we can calculate the distance as follows:
D=√52+42 = √41 ≈ 6.4

e. Using the Pythagorean theorem, we can calculate the distance as follows:
D=√12+82 = √65 ≈ 8.06

f. Using the Pythagorean theorem, we can calculate the distance as follows:
D=√32+12 = √10 ≈ 3.16

a. The distance is 8 units. See picture.

b. The distance is 20 units. See picture.

c. The distance is |b – a| units, where the vertical bars indicate absolute value. See picture.

d. The distance is |b – a| units. See picture.

Repeating the procedure from Problem C4, we see that the distance is as follows:
![]()

Since you get an answer that is non-negative whenever you square a number, it’s standard to write (x2-x1)2 rather than |x2-x1|2. The two expressions always give the same answer.