Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
In this part, we will begin to use segment notation. Optional: About Segment Notation (see below).
Let’s look again at how we solved Problem B3, in which we dissected a triangle to form a parallelogram. Note 4
Find the midpoints of two sides of a triangle. Cut along the segment connecting those two midpoints.
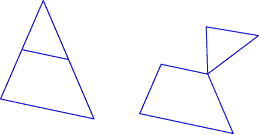
Rotate the top triangle 180° about one of the midpoints.

The two segments match because the cut was at the midpoint. The following are the conjectures that we will prove in the midline theorem:
Here are examples of midline cuts for four triangles (regular, right, isosceles, obtuse):
| Triangle | Midline Cut | Rotate Top Triangle |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
About Segment Notation
In mathematics, we make a distinction between an object and a measurement taken on that object. In the tradition of mathematicians being careful with their words and notation, this distinction carries over into how we write the names of things. For example:
![]() refers to the segment with endpoints X and Y. The line over the letters tells you that we’re talking about a segment, not a line or a ray.
refers to the segment with endpoints X and Y. The line over the letters tells you that we’re talking about a segment, not a line or a ray.
XY, on the other hand, refers to the length of the segment with endpoints X and Y. The lack of segment (or line or ray) markings above the letters changes the meaning. We’re no longer talking about the object itself, but about a property of that object (namely, its length).
This distinction continues when comparing segments. We say that two segments are congruent, so we use the segment notation
XY ≅AB
But we say that two lengths are equal, so we use the length notation
XY = AB
or
XY = 3 inches
The statements XY ≅AB and XY = AB convey exactly the same information, but one is talking about segments and the other about lengths.
We make a similar distinction between angles and their measures. Thus, angles are congruent:
∠XYZ ≅∠ABC
But their measures are equal:
m∠XYZ ≅∠ABC
or
m∠XYZ ≅∠ABC
The midline theorem claims that cutting along the midline of a triangle creates a segment that is parallel to the base and half as long. Does that seem reasonable?
To prove the midline cut works, you need to use some geometry facts that you may already have encountered. If not, take some time to consider why these statements are true. (Note 5)
Fact 1: Vertical angles (the angles opposite each other when two lines intersect) are congruent (they have the same measure).

Why: We can show why, for example, m∠1 = m∠3:
m∠1 + m∠2 = 180° and m∠2 + m∠3 = 180°, since in both cases the two angles together create a “straight angle.” So m∠1 + m∠2 = m∠2 + m∠3 = 180°. Subtracting m∠2 from each part of the equation, we see that
m∠1 = m∠3 = 180° – m∠2.
Fact 2: If two triangles have two sides that are the same length, and the angle between those two sides has the same measure, then the two triangles are congruent. The two triangles must have the same size and shape, so all three sides have the same length, and all three angles have the same measure. This is known as SAS (side-angle-side) congruence.

The single tick indicates the two sides that are the same length.
The double tick indicates the two sides that are the same length.
The angle markings indicate that those two angles have the same measure.
Why: The easiest way to be convinced of the fact that the two triangles are congruent is to draw some triangles. Draw a segment 2 inches long and a segment 3 inches long, with a 60° angle between them. Is there more than one way to complete the triangle? Come up with other cases to try.
Fact 3: There are many equivalent definitions of “parallelogram”:
You may want to print this page for use in the problems that follow.
With these facts in mind, let’s prove that the midline cut works.
Cutting along the midline of a triangle creates a segment that is parallel to the base and half as long.
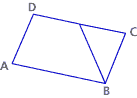
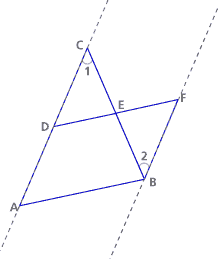
Start with this picture. It was created so that D and E are midpoints of AC and BC respectively. D, E, and F are collinear (on the same line), and DE and EF are the same length. Note 6

Considering the facts in the previous tab, explain why triangles DEC and FEB are congruent.
Explain why AD and BF have the same length.
Explain why AD and BF are parallel.
![]() Look at the angles marked 1 and 2 in the picture below.
Look at the angles marked 1 and 2 in the picture below.

Explain why ABFD is a parallelogram.
Explain why DE is parallel to AB and half as long.
By proving the midline theorem — since we proved it, we can call it a theorem now — we illustrate some important mathematical ideas.
Video SegmentBeing able to make these kinds of proofs can be a useful skill in the professional world. In this segment, Mr. Ialeggio explains how, in order to ensure accurate dimensions, he proves that the window frames he makes for antique homes are indeed rectangles. You can find this segment on the session video approximately 23 minutes and 29 seconds after the Annenberg Media logo. |
Take it Further
![]() Consider the diagonal AC and its relationship to the segments in question.
Consider the diagonal AC and its relationship to the segments in question.
In the picture below, AB equals BC, and AD equals CD. Explain why EF is parallel to HG and why they are the same length. What kind of quadrilateral is EFGH?

Draw another quadrilateral and connect the midpoints of the four sides in order. What kind of quadrilateral is formed and why? Note 7
Problem C1-C6 adapted from Connected Geometry, developed by Educational Development Center, Inc. pp.194-195. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
If you are working in a group, check to see if anyone used a cutting method similar to the one presented here. If so, consider using their method to launch the proof rather than the one shown here.
Spend a few minutes reflecting on or discussing each fact. If you are working in a group, it may help to have posters of these that everyone can refer to as they work on the proofs.
It’s sometimes hard for people to separate this figure from the cutting activities they’ve just been engaged with. Make sure you’re clear about how the figure was constructed; it might help to create it yourself. First, start with the triangle. Find midpoints D and E and connect them. Then extend that segment to twice its length. Recall what we know: AD = DC (D is a midpoint); BE = EC (E is a midpoint); DE = EF (we made the figure that way); angle DEF is 180° (we made it a straight line). That’s all we know.
You may have already made a conjecture about this situation in the Take It Further section of Session 4. Now you have the tools to actually prove it.
By construction, E is a midpoint of BC, so the sides CE and EB are congruent. Similarly, the sides DE and EF are congruent. By Fact 1, the angles between the congruent pairs of sides are equal, since they are vertical angles (the two angles at the shared vertex E). Then, by Fact 2, the two triangles are congruent.

Since the triangles DEC and FEB are congruent (by Problem C1), the corresponding sides in the two triangles are congruent. In particular, DC and FB have the same length. But DC has the same length as AD, since, by construction, D is the midpoint of AC. Therefore, AD and BF have the same length.

The angles DCE and FBE have the same measure since they are corresponding angles in congruent triangles. If we extend line segments DC and FB into lines, the two angles become alternate interior angles along a transversal to the two lines. Since the alternate interior angles are congruent if and only if the two lines are parallel, we conclude that the two lines and the segments on them are indeed parallel. So we have shown that the segments AD and BF are parallel.

By Problems C2 and C3, we know that the segments AD and BF have the same length and are parallel. They are also opposite sides in the quadrilateral ABFD. Since we have one pair of opposite sides congruent and parallel, we can use the fourth definition in Fact 3 to conclude that ABFD is a parallelogram.

Since AB and DF are opposite sides of a parallelogram (by Problem C4), they are parallel. We also know that DE lies on DF since the points D, E, and F all lie on the same line (by construction). Therefore, DE is also parallel to AB.
Finally, since AB and DF are opposite sides of a parallelogram (by problem C4), they must have the same length. Also, DE and EF have the same length by our construction. This means that DE must be half as long as DF (which is DE + EF). Since DE is half as long as DF, it is also half as long as AB.

Since EF is a midline of ABC, EF is parallel to AC and half the length of AC. Similarly, since HG is a midline of ACD, HG is parallel to AC and half its length. So EF and HG are parallel (since they are both parallel to AC) and of equal length (since they are both half the length of AC). The quadrilateral EFGH is a parallelogram, by Fact 3, since it has a pair of congruent and parallel opposite sides, namely EF and HG.
Thinking even more deeply, you might notice that ABCD was constructed to be a kite, so its diagonals are perpendicular. Therefore, the sides of the inside quadrilateral — each parallel to one of the diagonals of ABCD — are also perpendicular to each other. So, in fact, EFGH is a rectangle (a special kind of parallelogram).

Using similar reasoning from Problem C6, you can prove that the inscribed quadrilateral must always be a parallelogram. In the diagram below, construct the diagonal BD. Using this diagonal as the base of two triangles (BDC and BDA), we have two triangles with midlines: FG is the midline of triangle BDC, and EH is the midline of triangle BDA. Each midline is parallel to the base, so FG and EH must be parallel to one another. By a similar argument (using diagonal AC), we can say that EF and HG must each be parallel to AC, and therefore parallel to one another. Then, definition 1 in Fact 3 tells us that EFGH must be a parallelogram, no matter how the original quadrilateral is constructed.

Note that for some concave quadrilaterals we can get the sides of the interior quadrilateral to coincide, so it’s not really a parallelogram. Except in those rare cases, it will be a parallelogram.