Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Private: Learning Math: Geometry
The Pythagorean Theorem Part B: Proving the Pythagorean Theorem (65 minutes)
Session 6, Part B
In this part
- What Is a Theorem?
- Constructing a Proof
- More Proofs
What Is a Theorem
A theorem in mathematics is a proven fact. A theorem about right triangles must be true for every right triangle; there can be no exceptions. Just showing that an idea works in several cases is not enough to make an idea into a theorem.
The Pythagorean theorem has been proven to work for every possible right triangle. Of course, you can’t draw every right triangle on graph paper, make squares on the sides, and find their areas.
Many people have written proofs of the Pythagorean theorem. In fact, whole books exist that contain nothing but proofs of this one theorem! The proof that follows is probably from China, about 200 B.C.E. Rather than learning of it from the Pythagoreans, though, the author of the proof most likely developed the theorem independently.
Constructing a Proof
For the proof outlined below, follow the directions at each step, and answer the questions as you work. When you are finished, you will have constructed a proof of the Pythagorean theorem. Note 2
Step 1: Construct an arbitrary right triangle that is not isosceles. Label the short leg a, the long leg b, and the hypotenuse c.
The proof still works if the triangle is isosceles — that is if a = b — but it is always better to work through a proof with an example that is not special in any way.
Step 2: Construct two squares whose sides have length a + b.
 |
|
Step 3: Dissect one of the squares as shown below:
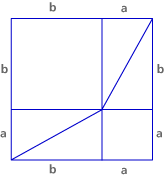
This dissection yields a square with side length a in one corner, a square with side length b in the opposite corner, and two rectangles, each cut along one diagonal into two right triangles.
Problem B1
Show that each of the four triangles you have just created is congruent to the original right triangle.
Step 4: Dissect the other square as shown below:
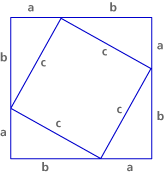
This dissection yields four triangles congruent to the original right triangle and a remaining piece in the center.
Try to show that the piece’s angles must all be right angles.
Problem B2
Show that the piece in the center is a square with side length c.
Step 5: The two original squares have the same area.
The eight triangles are congruent. So the four from the first square are equal in area to the four from the second square.
|
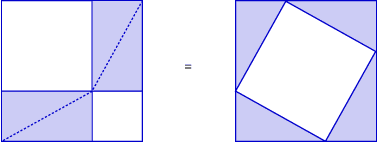
Shaded Area Here |
Equals |
Shaded Area Here |
Step 6: Remove the four triangles from each square. What remains in the first square will have the same area as what remains in the second square.
|
Unshaded Area Here |
Equals |
Unshaded Area Here |
The geometric equality — the Pythagorean theorem, as Euclid knew it — has been shown.
Our more modern algebraic interpretation, a2 + b2 = c2, follows from the algebraic formulas for the areas of the squares. The areas of the two squares on the left are a2and b2. The area of the square on the right is c2. Geometric reasoning tells you that the areas on the left (a2 + b2) and right (c2) are equal.
 |
Video Segment
In this video segment, the participants help demonstrate why a2, b2, and c2 are all squares with 90° angles at their vertices. Was your method similar to the one shown here? If not, in what ways was it different? You can find this segment on the session video approximately 10 minutes and 51 seconds after the Annenberg Media logo. |
Part B: Constructing a Proof, Steps 1-6 adapted from Connected Geometry, developed by Educational Development Center, Inc. pp. 198, 199, 200. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
More Proofs
Below are two more proofs of the Pythagorean theorem, but only the pictures are given to you.
Think about the first picture as two squares together. What are the new side lengths of the two squares?
Problem B3
This is a famous one-word proof written by the Hindu mathematician Bhaskara Acharya (1114-1185). What is the reasoning behind his proof?
 |
 |
Behold! |
Compute the area of the figure two ways — first by finding and adding the area of the three triangles and second by using the formula for the area of a trapezoid (1/2 • (sum of bases • height)). What must be true of the two areas you computed?
Problem B4
James Garfield (1831-1881) was the 20th president of the United States. Five years before becoming president, he discovered this proof of the Pythagorean theorem. What is the reasoning behind his proof?
 |
Problems B3 and B4 adapted from Connected Geometry, developed by Educational Development Center, Inc. pp. 198, 202. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
Notes
Note 2
Use graph paper to construct this proof. If you are working in a group, have everyone follow the steps as a whole group. You can choose to display a poster for Step 6 to help in the explanation.
Solutions
Problem B1
By construction, all four triangles are right triangles. The longer leg of each triangle has length b (since it equals the length of the side of the larger inscribed square), and the shorter leg of each triangle has length a (since it equals the length of the side of the smaller inscribed square). So all four triangles have two congruent sides as well as the angle between the two sides. So, by SAS congruence, the four triangles are indeed congruent to the original.
Problem B2
The sides of the piece in the center are all equal to c, since they are the longest sides of four triangles that are congruent to the original triangle (see the argument of Problem B1). Now we have to show that the angles are each 90°. Notice that three angles line up to make a straight line, or 180°: the small and the middle angles from the original right triangle (marked with one and two lines, respectively), and the one from the quadrilateral that lies between the two (see picture). Since the three angles of a triangle also add up to 180°, the angle in the quadrilateral must be the same as the largest angle in the triangle — a right angle. This is true for all four angles in the shape, and so we know that we have a quadrilateral with four congruent sides and four right angles, so it must be a square.
Problem B3
The larger (shaded) square has side b, so its area is b2 (see picture below). The smaller square has side a, so its area is a2. The pieces that make up all of this are four right triangles with sides a and b, and a small square with side b – a. (It is the difference between the side b square and the smaller side of the triangle.) The same five pieces make up the large square with area c2 in the third picture. So a2 + b2 = c2.
 |
|
 |
 |
||
Problem B4
The picture shows a trapezoid made up of three triangles. The areas of the triangles are ab / 2 (two of them), and c2 / 2. On the other hand, using the formula for the area of the trapezoid, we get that the overall area is (a + b)(a + b) / 2. So:
ab / 2 + ab / 2 + c2 / 2 = (a + b)2 / 2
Multiplying both sides by 2 and expanding the right-hand side, we get the following:
2ab + c2 = a2 + 2ab + b2
or
a2 + b2 = c2
