Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
A cross section is the face you get when you make one slice through an object. Below is a sample slice through a cube, showing one of the cross sections you can get.

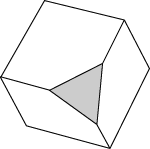
The polygon formed by the slice is the cross section. The cross section cannot contain any piece of the original face; it all comes from “inside” the solid. In this picture, only the gray piece is a cross section.
Use the Interactive Activity below to work on Problems C1 and C2. For a non-interactive version of the activity, and to work on Problems C3 and C4, you may want to use clay solids and dental floss to derive your answers. Alternatively, you may want to use colored water in plastic solids. Note 3
![]() How may faces does a cube have? Each side of your cross section comes from cutting through a face of your cube.
How may faces does a cube have? Each side of your cross section comes from cutting through a face of your cube.
Try to make the following cross sections by slicing a cube:
| a. | a square |
| b. | an equilateral triangle |
| c. | a rectangle that is not a square |
| d. | a triangle that is not equilateral |
| e. | a pentagon |
| f. | a hexagon |
| g. | an octagon |
| h. | a parallelogram that is not a rectangle |
| i. | a circle |
Record which of the shapes you were able to create and how you did it. The Interactive Activity provides you with one way to make each of the shapes that you can, in fact, make as a cross section.
A couple of the shapes on the list in Problem C1 are impossible to make by slicing a cube. Explain what makes them impossible.
Find a way to slice a tetrahedron to make a square cross section. How did you do it?

What cross sections can you get from each of these figures?

Cross Sections adapted from Connected Geometry, developed by Educational Development Center, Inc. © 2000 Glencoe/McGraw-Hill. Used with permission. www.glencoe.com/sec/math
You’ve looked at some of the “two-dimensional” properties of three-dimensional figures: their surfaces (nets) and their cross sections. Solid figures also cast two-dimensional shadows. Do you think you can recreate a solid by knowing what shadows it casts?
A solid object casts a circular shadow on the floor. When it is lit from the front, it casts a square shadow on the back wall. Try to build the object out of clay. Can you name it?

A solid object casts a circular shadow on the floor. When it is lit from the left, it casts a triangular shadow on the back wall. Try to build the object out of clay. Can you name it?

Suppose the object casts a circular shadow on the floor, a square shadow when lit from the front, and a triangular shadow when lit from the left. Try to build the object out of clay. Can you name it? Note 4

To use clay solids and dental floss to derive your answers, mold a cube from the clay. Then use the dental floss or piano wire to make a straight slice through the cube, creating a cross section. When making a cut, you may end up with “bent” cuts, but what you want to try to make is a planar slice. For example, think about slicing straight through a loaf of bread.
Alternatively, you may want to use colored water in plastic solids. Fill the plastic solids part way, and then tilt them at different angles to see the faces of cross sections created by an imaginary slice along the surface of the water.
You may want to further explore Problems C5-C7 on your own using a flashlight and objects described in solutions to these problems.
Problem C1
| a. | A square cross section can be created by slicing the cube by a plane parallel to one of its sides.
|
|||
| b. | An equilateral triangle cross section can be obtained by cutting the cube by a plane defined by the midpoints of the three edges emanating from any one vertex.
|
|||
| c. | One way to obtain a rectangle that is not a square is by cutting the cube with a plane perpendicular to one of its faces (but not perpendicular to the edges of that face), and parallel to the four, in this case, vertical edges.
|
|||
| d. | Pick a vertex, let’s say A, and consider the three edges meeting at the vertex. Construct a plane that contains a point near a vertex (other than vertex A) on one of the three edges, a point in the middle of another one of the edges, and a third point that is neither in the middle nor coinciding with the first point. Slicing the cube with this plane creates a cross section that is a triangle, but not an equilateral triangle; it is a scalene triangle. Notice that if any two selected points are equidistant from the original vertex, the cross section would be an isosceles triangle.
|
|||
| e. | To get a pentagon, slice with a plane going through five of the six faces of the cube.
|
|||
| f. | To get a hexagon, slice with a plane going through all six faces of the cube.
|
|||
| g. | It is not possible to create an octagonal cross section of a cube. | |||
| h. | To create a non-rectangular parallelogram, slice with a plane from the top face to the bottom. The slice cannot be parallel to any side of the top face, and the slice must not be vertical. This allows the cut to form no 90° angles. One example is to cut through the top face at a corner and a midpoint of a non-adjacent side, and cut to a different corner and midpoint in the bottom face.
|
|||
| i. | It is not possible to create a circular cross section of a cube. |
Whenever we cut the cube with a plane, each edge of the cross section corresponds to an intersection of one of the cube’s faces with the plane. Since the cube has only six faces, it is impossible to cut it with one plane and create an octagonal cross section. Also, since the cube has no curved faces, a plane will not be able to intersect a cube and create a cross section with a curved segment in its perimeter.
One way to create a square cross section in a tetrahedron is to cut at the midpoints of four edges.
Alternatively, you can start with a net for the tetrahedron such as:

We then connect the midpoints of the sides with segments of equal length: EF, FG, GH, and HE.

When we fold the net into a tetrahedron, the points E, F, G, and H are on the same plane, and they define a square cross section when that plane cuts the tetrahedron.
| a. | Any cross section of a sphere will be a circle. |
| b. | Possible cross sections are circles (cut parallel to the base), rectangles, and ellipses. |
| c. | Possible cross sections are circles (cut parallel to the circular base), ellipses (cut at an angle, not parallel to the circular base and not intersecting the base of the cone), parabolas (cut parallel to the edge of the cone, not intersecting the vertex but intersecting the base), and hyperbolas (cut perpendicular to the base, but not intersecting the vertex). |
A right square cylinder, i.e., a cylinder whose height equals the diameter of its base.
A right circular cone.
It’s a solid that looks like a “triangular” filter for a coffee maker, or the head (not handle) of a flathead screwdriver.
