Surface Area

Rectangles

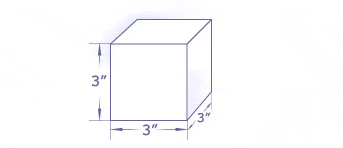
The surface area of a polyhedron is equal to the sum of the area of all of its faces. Said another way, the surface area is the total area covered by the net of a polyhedron. Let's take a look at a cube.

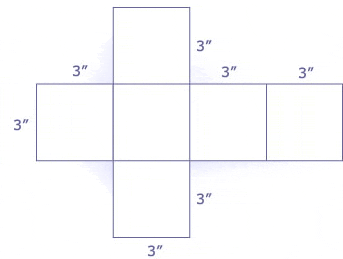
As you already know, a cube has six square faces. If each of those faces is 3 inches by 3 inches, then the area of each face is 3 × 3 = 9 square inches. And since there are six of them, the total surface area is 9 + 9 + 9 + 9 + 9 + 9 = 54 square inches.

To find the surface area of any shape, you can follow the process described below:

1. Draw a net of the polyhedron.
2. Calculate the area of each face.
3. Add up the area of all the faces.

But for many polyhedra, there are formulas that can be used to find the total surface area. For instance, the formula for the surface area of a cube is:

where s is the side length of the square faces.

Explore & Play with Surface Area

In the animation below, hit the play button to watch the net fold up into a three-dimensional prism. Hit the pause button at any time to freeze the animation. Then, in the diagram to the right, calculate and enter the value for each face of the prism. Upon hitting the enter key, if your calculation is wrong, your answer will appear in red and you will be given two hints and two more chances before the correct answer is displayed.