Euler's Theorem

You've already learned about many polyhedra properties. All of the faces must be polygons. Two faces meet along an edge. Three or more faces meet at a vertex.

In this lesson, you'll learn about a property of polyhedra known as Euler's Theorem, because it was discovered by the mathematician Leonhard Euler (pronounced "Oil-er"). You already know that a polyhedron has faces (F), vertices (V), and edges (E). But Euler's Theorem says that there is a relationship among F, V, and E that is true for every polyhedron. That's right — every polyhedron, from a triangular prism to a hexagonal pyramid to a truncated icosahedron.

Euler's Theorem actually played a role in a notable discovery. In some chemistry experiments, a group of researchers believed that they had found a new molecule with the exact weight of 60 carbon atoms. Although they couldn't see this molecule, they speculated that its shape was a truncated icosahedron — a "soccer ball" in which 60 carbon atoms (vertices) were joined together by 90 bonds (edges). From Euler's Theorem, they then knew that the atoms must be arranged to form a spherical soccer ball with 32 faces, some of them hexagons and some pentagons.

Discover this formula for yourself...

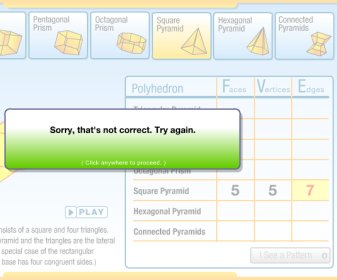In the activity below, choose a prism from the top row and then hit the play button to watch its net fold up to form the corresponding three-dimensional shape. Hit the pause button at any time to freeze the animation.

Use the animation to help you count the number of faces (F), vertices (V), and edges (E) for each prism. Then, enter these values into the appropriate boxes in the table to the right.

Fill in each square and press the enter/return key. Feedback will be given immediately. As in the other activities, if your calculation is wrong, your answer will appear in red and you will be given two hints and two more chances before the correct answer is displayed.

Look for a pattern in the row as you input numbers; after correctly completing three rows, you will be given an opportunity to express this pattern in an equation. Or, you may continue working on the table until you are able to identify the pattern.