Join us for conversations that inspire, recognize, and encourage innovation and best practices in the education profession.
Available on Apple Podcasts, Spotify, Google Podcasts, and more.
Look for the following topics in the video, indicated by the ![]() onscreen icon, and click below to learn more.
onscreen icon, and click below to learn more.
 Seeing the Shapes of Particles |
 Units of Pull |
The simple answer is “No.” When we see something, even with a very powerful microscope, what we are really seeing is the light that has come from some source (like the Sun or a glowing filament in a light bulb) “bounced” off the object and entered our eyes. Scientists call this bouncing “diffraction.”
Let’s look at an analogy. Imagine you are skiing down a hill and there’s a small patch of snow missing in front of your ski. If you have normal sized skis, you probably won’t notice the hole as you ski over it. You would have to have very tiny skis for your skis to be impacted, or to “see,” the missing snow.
In this analogy, the skis are light’s wavelength. Visible light has too long a wavelength to effectively interact with individual particles: they are like the normal size skis going over the small hole. If, however, we use light of a much shorter wavelength light, like x-rays, they can, in fact, interact with individual particles.

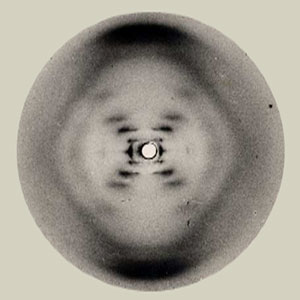
DNA molecule seen through x-ray diffraction.
In this process, x-rays are directed toward a macroscopic object and are diffracted by the small spaces between its individual particles. Depending on the size of those spaces, the x-rays will emerge from the macroscopic object in slightly different directions. If the pattern of these directions is recorded (e.g., with a photographic plate or specialized digital camera), a computer can then reconstruct what the spacing arrangement was. Once the packing arrangement and the spacing are determined, scientists can reconstruct the size and shape of the individual particles.
Since the image we get is not an actual photograph of what the particles look like, but rather a computer-generated model, x-ray diffraction is called an “indirect” imaging method, as opposed to a “direct” imaging method.

Science Studio push meter.
When the children in the Science Studio in Session 5 pushed the Styrofoam under the water, the scale read about 30 pounds. When they used the “pull meter” to pull the Styrofoam under the water, the instrument read 11 “somethings.” It was not clear what the unit was. In fact, both meters measure the same thing — force. Force is sometimes defined as “any kind of push or pull on an object.” The push meter measured force in pounds from the English system of measurement, while the pull meter measured force in Newtons from the metric system. One pound of force is equal to 4.4. Newtons. In general, when talking about force, it is equally correct to use Newtons and/or pounds as units.
If pounds are a unit of force in the English system and Newtons are the unit of force in the metric system, where do kilograms fit in? This is sometimes a confusing issue in introductory science. The bottom line can be put into one sentence: In the United States, we (incorrectly) use a unit of force, the pound, when we are really talking about an object’s mass.
Recall that mass is a measure of the amount of matter in an object. Another equally good definition is “the measure of an object’s resistance to motion” (i.e., a measure of its inertia). This amount of matter in an object is not defined in terms of any forces at all, and so there are different units for mass. In the metric system, the unit of mass is the gram; in the English system, the unit of mass is the slug.
We know that forces are defined as pushes or pulls. If weight is a force, where does the pull come from? The answer is gravity. Every piece of matter in the universe pulls on every other piece of matter with a gravitational force. As you sit reading this sentence, every other piece of matter in the universe is pulling you toward it: your coffee cup, your neighbor’s lawnmower, the Empire State Building, the Sun, and even a galaxy halfway across the universe. However, by far the largest gravitational force that acts on you is the pull toward the Earth, because it is so big and so close. The other forces add very little to the total gravitational force you feel. It is the gravitational force from the Earth that we call “weight.”
Let’s look at an example. When astronauts visited the moon, their mass (i.e., the amount of matter in their bodies) did not change. However, because the Moon has less mass than the Earth, it generates less gravitational force. As a result, the astronauts on the Moon had less force acting on them and, therefore, their weight on the Moon would have been less than their weight on the Earth. Weight is a measurement of the amount of force, i.e., the pull being exerted on an object, and mass is a measurement of the amount of matter in an object.
It would be more precise if we replaced the word “weight” with the phrase “gravitational force due to Earth” but, in everyday language, we rarely need to make our meaning so exact. Language in science, however, is designed to be more precise than everyday language. Certain words carry specific meaning, and we must be aware of those meanings when we look to communicate in a scientific way.
